题目内容
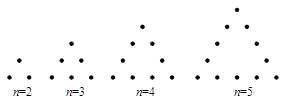
如下图所示将若干个点摆成三角形图案,每条边(包括两个端点)有n(n>l,n∈N*)个点,相应的图案中总的点数记为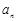 ,则
,则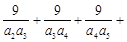 …
…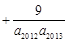 =
= 
A.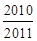 | B.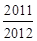 | C.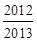 | D.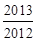 |
B
解析试题分析:每个边有n个点,把每个边的点数相加得3n,这样角上的点数被重复计算了一次,故第n个图形的点数为3n-3,即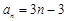 .令
.令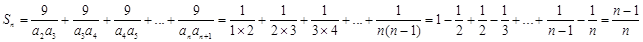
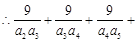 …
…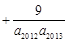 =
=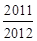 ,故选B..
,故选B..
考点:1.归纳推理;2.数列的求和..

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
已知数列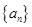 ,
,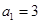 ,
,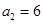 ,且
,且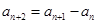 ,则数列的第五项为( )
,则数列的第五项为( )
A. | B.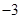 | C.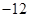 | D.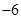 |
已知数列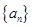 的前n项和
的前n项和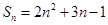 ,则
,则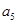 的值为 ( )
的值为 ( )
| A.20 | B.21 | C.22 | D.23 |
若数列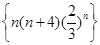 中的最大项是第
中的最大项是第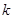 项,则
项,则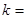 ( )
( )
| A.4 | B.5 | C.6 | D.7 |
数列 的首项为
的首项为 ,
, 为等差数列且
为等差数列且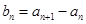 .若
.若 ,
,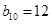 ,则
,则 ( )
( )
A. | B. | C. | D. |
无穷数列1,3,6,10……的通项公式为( )
| A.an=n2-n+1 | B.an=n2+n-1 |
C.an= | D.an= |
已知数列 满足
满足 ,
, ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
数列{an}满足an+1+(-1)nan=2n-1,则{an}的前60项和为( )
| A.3690 | B.3660 | C.1845 | D.1830 |
数列{an}中,an=-2n2+29n+3,则此数列最大项的值是( )
| A.103 | B.108 | C.103 | D.108 |