题目内容
设 表示数列
表示数列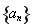 的前
的前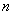 项和.
项和.
(1)若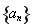 为公比为
为公比为 的等比数列,写出并推导
的等比数列,写出并推导 的计算公式;
的计算公式;
(2)若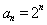 ,
,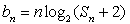 ,求证:
,求证: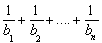 <1.
<1.
【答案】
(1) ;(2)证明过程详见试题解析.
;(2)证明过程详见试题解析.
【解析】
试题分析:(1)利用错位相减法进行推导,先写出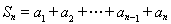 ,然后将此式两边同时乘以公比
,然后将此式两边同时乘以公比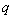 ,得到
,得到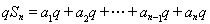 ,两式相减可得:
,两式相减可得: ,所以当
,所以当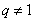 时,有
时,有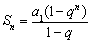 ,但是要注意当
,但是要注意当 时,
时, ;(2)若
;(2)若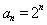 ,
, ,那么
,那么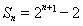 ,所以
,所以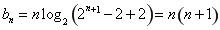 .注意到
.注意到 ,证明过程中采用裂项相消法进行,有
,证明过程中采用裂项相消法进行,有 .
.
试题解析:(1)因为
所以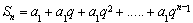 ①
①
将①式乘以公比 ,可得
,可得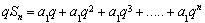 ②
②
①-②得: 
所以当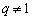 时,
时,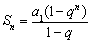
当 时,
时,
因此
(2)证明:因为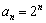 ,所以
,所以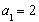 ,
,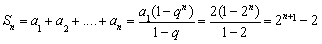
所以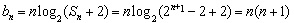
因此
则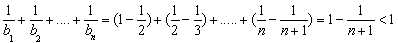
考点:等比数列前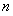 项和;数列不等式证明.
项和;数列不等式证明.

练习册系列答案
相关题目
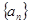 的前
的前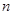 项和为
项和为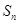 ,首项
,首项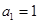 ,点
,点 在曲线
在曲线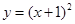 上.
上.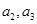 ;
;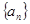 的通项公式
的通项公式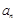 ;
;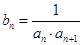 ,
,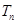 表示数列
表示数列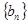 的前项和,若
的前项和,若 恒成立,求
恒成立,求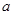 的取值范围.
的取值范围.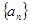 中,
中,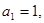 且点
且点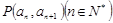 在直线
在直线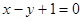 上.
上.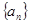 的通项公式;
的通项公式; (2)若函数
(2)若函数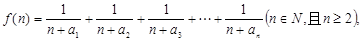 求函数
求函数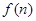 的最小值;
的最小值; 表示数列
表示数列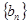 的前
的前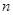 项和.试问:是否存在关于
项和.试问:是否存在关于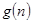 ,使得
,使得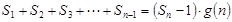 对于一切不小于2的自然数
对于一切不小于2的自然数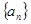 中,
中,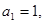 且点
且点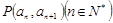 在直线
在直线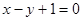 上.
上.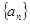 的通项公式;
的通项公式;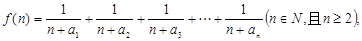
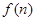 的最小值;
的最小值;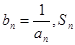 表示数列
表示数列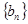 的前
的前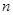 项和.试问:是否存在关于
项和.试问:是否存在关于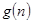 ,使得
,使得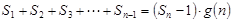 对于一切不小于2的自然数
对于一切不小于2的自然数