题目内容
已知定义在 上的两个函数
上的两个函数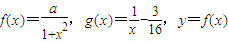 的图象在点
的图象在点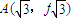 处的切线的斜率为
处的切线的斜率为 .
.(1)求f(x)的解析式;
(2)试求实数k的最大值,使得对任意
 恒成立;
恒成立;(3)若
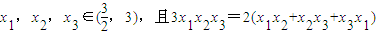 ,求证:
,求证: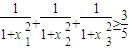 .
.
【答案】分析:(1)求f′(x),进一步求出f′(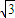 ),令其等于-
),令其等于-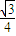 ,得a值,代入得f(x)的解析式;
,得a值,代入得f(x)的解析式;
(2)把解析式代入不等式,观察f(x)、g(x)均为正数,分离参数,设另一边为函数h(x),求其导函数,令h′(x)>0,令h′(x)<0,得函数h(x)的单调性,进一步求出其最大值,代入不等式可求k的范围,即得k的最大值.
(3)由(2)的结论可得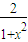 ≥
≥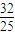 (
(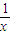 -
-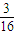 ),在上式中分别令x=x1,x2,x3,三式左右两边分别相加得一不等式,通分,结合所给等式,可得所求结果.
),在上式中分别令x=x1,x2,x3,三式左右两边分别相加得一不等式,通分,结合所给等式,可得所求结果.
解答:解:(1)由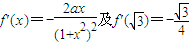
即可求得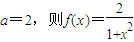 ;(3分)
;(3分)
(2)当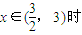 ,
,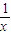 >
> >
>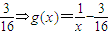 >0,
>0,
不等式f(x)≥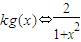 ≥
≥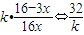 ≥
≥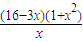 (5分)
(5分)
令
由于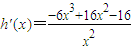 =
=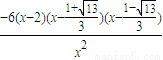 (7分)
(7分)
当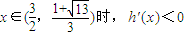 ;
;
当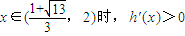 ;
;
当x∈(2,3)时,h'(x)<0.
又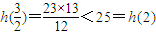 ,
,
故h(x)max=h(2)=25,
于是由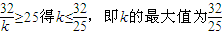 ;(10分)
;(10分)
(3)由(2)知,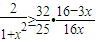
在上式中分别令x=x1,x2,x3再三式作和即得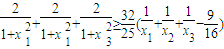 =
=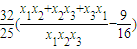 =
=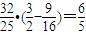 ,
,
所以有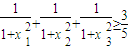 .(14分)
.(14分)
点评:本题考查导数在最大值问题中的应用,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.掌握不等式恒成立时所取的条件;
证明不等式一般会用到上面的结论,仔细观察要证式子及已证式子的特点,两者如何连接.
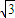 ),令其等于-
),令其等于-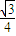 ,得a值,代入得f(x)的解析式;
,得a值,代入得f(x)的解析式;(2)把解析式代入不等式,观察f(x)、g(x)均为正数,分离参数,设另一边为函数h(x),求其导函数,令h′(x)>0,令h′(x)<0,得函数h(x)的单调性,进一步求出其最大值,代入不等式可求k的范围,即得k的最大值.
(3)由(2)的结论可得
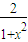 ≥
≥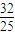 (
(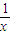 -
-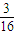 ),在上式中分别令x=x1,x2,x3,三式左右两边分别相加得一不等式,通分,结合所给等式,可得所求结果.
),在上式中分别令x=x1,x2,x3,三式左右两边分别相加得一不等式,通分,结合所给等式,可得所求结果.解答:解:(1)由
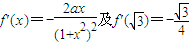
即可求得
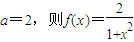 ;(3分)
;(3分)(2)当
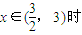 ,
,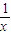 >
> >
>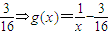 >0,
>0,不等式f(x)≥
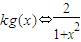 ≥
≥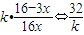 ≥
≥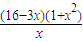 (5分)
(5分)令

由于
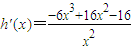 =
=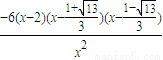 (7分)
(7分)当
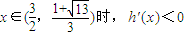 ;
;当
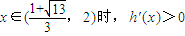 ;
;当x∈(2,3)时,h'(x)<0.
又
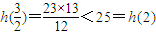 ,
,故h(x)max=h(2)=25,
于是由
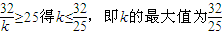 ;(10分)
;(10分)(3)由(2)知,
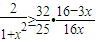
在上式中分别令x=x1,x2,x3再三式作和即得
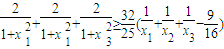 =
=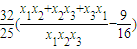 =
=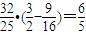 ,
,所以有
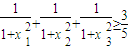 .(14分)
.(14分)点评:本题考查导数在最大值问题中的应用,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.掌握不等式恒成立时所取的条件;
证明不等式一般会用到上面的结论,仔细观察要证式子及已证式子的特点,两者如何连接.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目

 的单调性;
的单调性;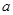 的取值范围;
的取值范围;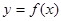 对于区间D上的任意两个值x1、x2总有以下不等式
对于区间D上的任意两个值x1、x2总有以下不等式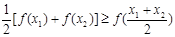 成立,则称函数
成立,则称函数 ,试判断函数
,试判断函数 满足
满足 ,
, 为
为 的图象如图所示,若两个正数
的图象如图所示,若两个正数 满足
满足 ,则
,则 的取值范围是
的取值范围是 B、
B、
 D、
D、

 上的函数
上的函数 满足
满足 ,
, 为
为 的图像如图所示,若两个正数
的图像如图所示,若两个正数 、
、 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C.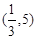 D.
D.
