题目内容
一个文艺团体下基层进行宣传演出,准备的节目表中原有4个歌手演唱,如果保持着演唱的相对顺序不变,拟再添加2个小品节目,则不同的节目表可排出
- A.20种
- B.25种
- C.30种
- D.32种
C
解析:
分析:4个歌手演唱,可产生5个空位,第一个小品可插入到其中的任何一个位置,第一个小品插入后,5个节目会产生6个空位,第二个小品可插入其一,由乘法原理即可解决问题.
解答:∵4个歌手可产生5个空位,保持着演唱的相对顺序不变,第一个小品可插入到其中的任何一个位置,有C51种方法,当第一个小品插入后,5个节目会产生6个空位,第二个小品可插入其一,仍然能保持着演唱的相对顺序不变,有C61种方法,根据乘法原理,不同的节目表可排出C51•C61=30种.故选C.
点评:本题考查排列、组合及简单计数问题,关键是对题意的正确理解及分步计数原理的正确应用,属于中档题.
解析:
分析:4个歌手演唱,可产生5个空位,第一个小品可插入到其中的任何一个位置,第一个小品插入后,5个节目会产生6个空位,第二个小品可插入其一,由乘法原理即可解决问题.
解答:∵4个歌手可产生5个空位,保持着演唱的相对顺序不变,第一个小品可插入到其中的任何一个位置,有C51种方法,当第一个小品插入后,5个节目会产生6个空位,第二个小品可插入其一,仍然能保持着演唱的相对顺序不变,有C61种方法,根据乘法原理,不同的节目表可排出C51•C61=30种.故选C.
点评:本题考查排列、组合及简单计数问题,关键是对题意的正确理解及分步计数原理的正确应用,属于中档题.

练习册系列答案
相关题目
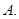 20种
20种 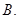 25种
25种 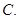 30种
30种 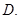 32种
32种