题目内容
已知直线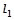 :x+ay+6=0和
:x+ay+6=0和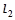 :(a-2)x+3y+2a=0,则
:(a-2)x+3y+2a=0,则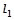 ∥
∥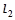 的充要条件是a=( )
的充要条件是a=( )
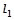 :x+ay+6=0和
:x+ay+6=0和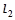 :(a-2)x+3y+2a=0,则
:(a-2)x+3y+2a=0,则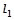 ∥
∥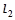 的充要条件是a=( )
的充要条件是a=( )| A.3 | B.1 | C.-1 | D.3或-1 |
C
分析:首先由两直线平行可得1×3=a×(a-2),解可得a=-1或3,分别验证可得a=-1时,则l1∥l2,即可得l1∥l2?a=-1;反之将a=-1代入直线的方程,可得l1∥l2,即有a=-1?l1∥l2;综合可得l1∥l2?a=-1,即可得答案.
解答:解:根据题意,若l1∥l2,则有1×3=a×(a-2),解可得a=-1或3,
反之可得,当a=-1时,直线l1:x-y+6=0,其斜率为1,直线l2:-3x+3y-2=0,其斜率为1,且l1与l2不重合,则l1∥l2,
当a=3时,,直线l1:x+3y+6=0,直线l2:x+3y+6=0,l1与l2重合,此时l1与l2不平行,
l1∥l2?a=-1,
反之,a=-1?l1∥l2,
故l1∥l2?a=-1,
故选C.
解答:解:根据题意,若l1∥l2,则有1×3=a×(a-2),解可得a=-1或3,
反之可得,当a=-1时,直线l1:x-y+6=0,其斜率为1,直线l2:-3x+3y-2=0,其斜率为1,且l1与l2不重合,则l1∥l2,
当a=3时,,直线l1:x+3y+6=0,直线l2:x+3y+6=0,l1与l2重合,此时l1与l2不平行,
l1∥l2?a=-1,
反之,a=-1?l1∥l2,
故l1∥l2?a=-1,
故选C.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 ”是“
”是“ 且
且 ”的 ( )
”的 ( ) 是互不相同的空间直线,
是互不相同的空间直线, 是不重合的平面,下列命题正确的是 ( )
是不重合的平面,下列命题正确的是 ( ) ,则
,则
 ,则
,则
 ,则
,则
 ,则
,则
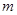 、
、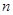 为两条不同的直线,
为两条不同的直线,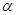 、
、 为两个不同的平面,且
为两个不同的平面,且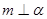 ,
,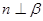 ,
,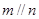 ,则
,则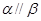 ②若
②若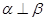 ,则
,则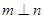
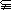 B”;
B”;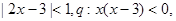 则p是q的( )
则p是q的( )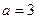 ”是“两直线
”是“两直线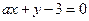 和
和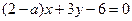 互相垂直”的( )
互相垂直”的( )