题目内容
1.如果双曲线的离心率e=$\frac{\sqrt{5}+1}{2}$,则称此双曲线为黄金双曲线.有以下几个命题:①双曲线$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{\sqrt{5}-1}=1$是黄金双曲线;
②双曲线y${\;}^{2}-\frac{2{x}^{2}}{\sqrt{5}+1}=1$是黄金双曲线;
③在双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$中,F1为左焦点,A2为右顶点,B1(0,b),若∠F1 B1 A2=90°,则该双曲线是黄金双曲线;
④在双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$中,过焦点F2作实轴的垂线交双曲线于M、N两点,O为坐标原点,若∠MON=120°,则该双曲线是黄金双曲线.
其中正确命题的序号为( )
| A. | ①和② | B. | ②和③ | C. | ③和④ | D. | ①和④ |
分析 对于①②求出双曲线的离心率判断正误;
对于③通过∠F1B1A2=90°,转化为a,b,c的关系,求出双曲线的离心率判断正误;
对于④,MN经过右焦点F2且MN⊥F1F2,∠MON=120°,转化为a,b,c的关系,求出双曲线的离心率判断正误.
解答 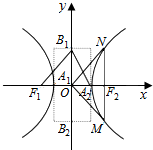 解:①双曲线$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{\sqrt{5}-1}=1$中a=$\sqrt{2}$,c=$\sqrt{\sqrt{5}+1}$,离心率是$\sqrt{\frac{\sqrt{5}+1}{2}}$,故不是黄金双曲线,即①不正确;
解:①双曲线$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{\sqrt{5}-1}=1$中a=$\sqrt{2}$,c=$\sqrt{\sqrt{5}+1}$,离心率是$\sqrt{\frac{\sqrt{5}+1}{2}}$,故不是黄金双曲线,即①不正确;
②由双曲线y${\;}^{2}-\frac{2{x}^{2}}{\sqrt{5}+1}=1$,可得离心率e=$\sqrt{1+\frac{\sqrt{5}+1}{2}}$=$\frac{\sqrt{5}+1}{2}$,故该双曲线是黄金双曲线,即②正确;
③∵∠F1B1A2=90°,∴$|{B}_{1}{F}_{1}{|}^{2}+|{B}_{1}{A}_{2}{|}^{2}=|{F}_{1}{A}_{2}{|}^{2}$,∴b2+c2+b2+a2=(a+c)2,化为c2-ac-a2=0,由③可知该双曲线是黄金双曲线;
④如图,MN经过右焦点F2且MN⊥F1F2,∠MON=120°,
∴NF2=$\sqrt{3}$OF2,∴$\frac{{b}^{2}}{a}=\sqrt{3}c$,∴b2=$\sqrt{3}$ac,∴c2-a2=$\sqrt{3}$ac,
∴e2-$\sqrt{3}$e-1=0,∴e=$\frac{\sqrt{3}±\sqrt{7}}{2}$,∴该双曲线不是黄金双曲线,
故选:B
点评 本题考查双曲线的基本性质,a,b,c的关系,离心率的求法,考查计算能力.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | 2 | D. | 2$\sqrt{3}$ |
| A. | 3:1 | B. | 3:4 | C. | 4:3 | D. | 1:3 |
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
 已知抛物线y2=2px的焦点为F,若该抛物线上有一点A,满足直线FA的倾斜角为120°,且|FA|=4,
已知抛物线y2=2px的焦点为F,若该抛物线上有一点A,满足直线FA的倾斜角为120°,且|FA|=4,