题目内容
 (2013•南通三模)如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等.
(2013•南通三模)如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等.(1)求证:AB∥平面PCD;
(2)求证:平面PAC⊥平面ABCD.
分析:(1)由矩形ABCD,对边平行得到AB∥CD,结合线面平行的判定定理得到AB∥平面PCD;
(2)连结BD,交AC于点O,连结PO,由在矩形ABCD中,点O为AC,BD的中点,可得PO⊥AC,PO⊥BD,进而由线面垂直的判定定理得到PO⊥平面ABCD,进而由面面垂直的判定定理得到平面平面PAC⊥平面ABCD.
(2)连结BD,交AC于点O,连结PO,由在矩形ABCD中,点O为AC,BD的中点,可得PO⊥AC,PO⊥BD,进而由线面垂直的判定定理得到PO⊥平面ABCD,进而由面面垂直的判定定理得到平面平面PAC⊥平面ABCD.
解答: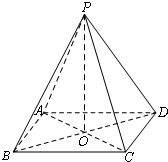 证明:(1)在矩形ABCD中,AB∥CD,
证明:(1)在矩形ABCD中,AB∥CD,
又AB?平面PCD,CD?平面PCD,
所以AB∥平面PCD. …(6分)
(2)如图,连结BD,交AC于点O,连结PO,
在矩形ABCD中,点O为AC,BD的中点,
又PA=PB=PC=PD,
故PO⊥AC,PO⊥BD,…(9分)
又AC∩BD=O,AC,BD?平面ABCD,
所以PO⊥平面ABCD,…(12分)
又PO?平面PAC,
所以平面PAC⊥平面ABCD. …(14分)
 证明:(1)在矩形ABCD中,AB∥CD,
证明:(1)在矩形ABCD中,AB∥CD,又AB?平面PCD,CD?平面PCD,
所以AB∥平面PCD. …(6分)
(2)如图,连结BD,交AC于点O,连结PO,
在矩形ABCD中,点O为AC,BD的中点,
又PA=PB=PC=PD,
故PO⊥AC,PO⊥BD,…(9分)
又AC∩BD=O,AC,BD?平面ABCD,
所以PO⊥平面ABCD,…(12分)
又PO?平面PAC,
所以平面PAC⊥平面ABCD. …(14分)
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,考查空间想象能力,属于中档题.

练习册系列答案
相关题目
 (2013•南通三模)根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内非正常行驶的机动车辆数为
(2013•南通三模)根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内非正常行驶的机动车辆数为