题目内容
已知数列: ,依它的前10项的规律,这个数列的第2011项a2011满足( )
,依它的前10项的规律,这个数列的第2011项a2011满足( )A.

B.

C.1≤a2011≤10
D.a2011>10
【答案】分析:第n组分母的规律为:1,2,3,…n,第n组分子的规律为:n,n-1,n-2,…2,1,所以数列的第2011项是数列第63组第58个数,即a2011=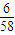 .
.
解答:解:因为数列的前10项为: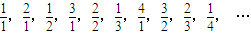 ,
,
所以分母的规律为:1;1,2;1,2,3;1,2,3,4;…,则第n组分母的规律为:1,2,3,…n,
分子的规律为:1;2,1;3,2,1;4,3,2,1;…,则第n组分子的规律为:n,n-1,n-2,…2,1,
所以数列的第2011项是数列第63组第58个数,即a2011=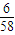 ,
,
所以 .
.
故选B.
点评:本题考查类比推理,是一个基础题,解题的关键是看清所给的几个元素之间的共性,要分清楚几种推理.
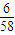 .
.解答:解:因为数列的前10项为:
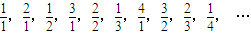 ,
,所以分母的规律为:1;1,2;1,2,3;1,2,3,4;…,则第n组分母的规律为:1,2,3,…n,
分子的规律为:1;2,1;3,2,1;4,3,2,1;…,则第n组分子的规律为:n,n-1,n-2,…2,1,
所以数列的第2011项是数列第63组第58个数,即a2011=
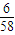 ,
,所以
 .
.故选B.
点评:本题考查类比推理,是一个基础题,解题的关键是看清所给的几个元素之间的共性,要分清楚几种推理.

练习册系列答案
相关题目
 ,依它的前10项的规律,这个数列的第2010项a2010=( )
,依它的前10项的规律,这个数列的第2010项a2010=( )



 ,依它的前10项的规律,这个数列的第2010项a2010=( )
,依它的前10项的规律,这个数列的第2010项a2010=( )



 ,依它的前10项的规律,这个数列的第2010项a2010满足( )
,依它的前10项的规律,这个数列的第2010项a2010满足( )

 ,依它的前10项的规律,这个数列的第2010项a2010满足( )
,依它的前10项的规律,这个数列的第2010项a2010满足( )
