Question

设的最大值为M。

   （1）当时，求M的值。

   （2）当取遍所有实数时，求M的最小值；

       （以下结论可供参考：对于，当同号时取等号）

   （3）对于第（2）小题中的，设数列满足，求证：。

Answer 1

（1）    （2）  （3）见解析

解析:

（1）求导可得

   

    当时取等号     3分

   （2）

       5分

   

    =6，

    。

    由（1）可知，当时，    。

          7分

   （3）证法一：（局部放缩法）因为，

    所以

    由于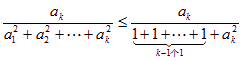

       9分

    所以不等式左边

   

   

        11分

    下证

    ，

    显然。即证。    12分

    证法二：（数学归纳法）即证：当

   

    下用数学归纳法证明：

    ①当时，左边，显然；

    ②假设时命题成立，即

      8分

    当时，

    左边

    （）

均值不等式

                   

         11分

    下证：（*）

    （*），

    显然。

    所以命题对时成立。

    综上①②知不等式对一切成立。     12分