题目内容
【题目】已知椭圆C： 
=1（a＞b＞0）的左、右焦点分别为F1 ， F2 ， 直线l经过F2且交椭圆C于A，B两点（如图），△ABF1的周长为4 
，原点O到直线l的最大距离为1．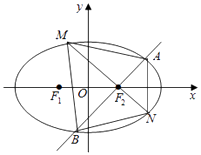 
（1）求椭圆C的标准方程；
（2）过F2作弦AB的垂线交椭圆C于M，N两点，求四边形AMBN面积最小时直线l的方程．
【答案】
（1）解：由题意知， 
，c=1，
∴ 
，
又∵a2=b2+c2，∴b=1，
∴椭圆C的标准方程为 
；
（2）解：当直线AB的斜率不存在时，
有 
， 
，∴ 
；
当直线AB的斜率为0时， ，∴ ；
当直线AB的斜率存在且不为0时，
设直线AB的方程为y=k（x﹣1），则直线MN的方程为 
，
联立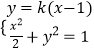 
得：（2k2+1）x2﹣4k2x+2k2﹣2=0．
设A（x1，y1），B（x2，y2），
则 
，
∴|AB|= 
= 
= 
．
同理|MN|= 
，
∴ 
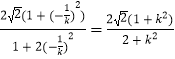|AB||MN|= 
，
令t=k2+1（t≥1）， 
，
当 
．即k2+1=2，即k=±1时， 
．
此时设直线AB的方程为y=±（x﹣1）
【解析】（1）由题意可得a，c的值，由隐含条件求得b的值，则椭圆方程可求；（2）分类求出直线AB的斜率不存在、斜率为0时的四边形AMBN面积，在设出斜率存在且不为0时的直线方程，联立直线方程和椭圆方程利用弦长公式求得|AB|、|MN|的长度，代入四边形面积公式，换元后利用配方法求得最值，同时得到边形AMBN面积最小时直线l的方程．
练习册系列答案
相关题目
