题目内容
某公司生产某种产品的固定成本为2万元,每生产一件产品增加投入150元,已知收益T(单位:元)满足T(x)=
,其中x是产品的月产量.
(Ⅰ)将利润W表示成月产量x的函数;
(Ⅱ)当月产量为多大时,公司的月利润最大?(收益=成本+利润)
|
(Ⅰ)将利润W表示成月产量x的函数;
(Ⅱ)当月产量为多大时,公司的月利润最大?(收益=成本+利润)
分析:(I)月利润W=月销售收入T(x)-生产仪器增加投入-固定成本;因T(x)是分段函数,故分别计算0≤x≤400,x>400 时,W的解析式;
(II)因为利润函数W是分段函数,所以要分别在0≤x≤400,x>400 时,计算W的最大值,通过比较得出W在其定义域上的最大值.
(II)因为利润函数W是分段函数,所以要分别在0≤x≤400,x>400 时,计算W的最大值,通过比较得出W在其定义域上的最大值.
解答:解:(I)当0≤x≤400 时,W=450x-
x2-20000-150x=-
x2+300x-20000;
当x>400 时,W=100000-20000-150x=-150x+80000;
综上所述:W=
.
(II)当0≤x≤400时,f(x)=-
(x-300)2+25000,
∴当x=300 时,f(x)max=25000;
当x>400 时,f(x)=-150x+80000 是减函数,
∴f(x)<-150×400+80000=20000;
综上所述,当x=300 时,Wmax=25000.
所以,当月产量为250台时,公司获得的月利润最大.
| 1 |
| 2 |
| 1 |
| 2 |
当x>400 时,W=100000-20000-150x=-150x+80000;
综上所述:W=
|
(II)当0≤x≤400时,f(x)=-
| 1 |
| 2 |
∴当x=300 时,f(x)max=25000;
当x>400 时,f(x)=-150x+80000 是减函数,
∴f(x)<-150×400+80000=20000;
综上所述,当x=300 时,Wmax=25000.
所以,当月产量为250台时,公司获得的月利润最大.
点评:本题考查了分段函数模型的应用,当分段函数求最值时,要分别在每一区间上求出最值,通过比较得出整个定义域上的最值.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
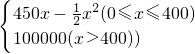 ,其中x是产品的月产量.
,其中x是产品的月产量.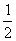
 ,其中x是产品的月产量.
,其中x是产品的月产量.