题目内容
(本小题满分12分)在直角坐标系XOY中,以O为极点,X轴正半轴为极轴建立极坐标系。曲线C的极坐标方程是: ,M,N分别是曲线C与X、Y轴的交点。
,M,N分别是曲线C与X、Y轴的交点。
(1)写出C的直角坐标系方程。并求M,N的极坐标。
(2)设MN的中点为P,求直线OP的极坐标方程。
(1)曲线C: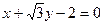 M(2,0) N(
M(2,0) N(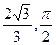 )
)
(2)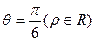 (说明:写成
(说明:写成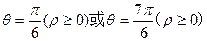 也正确)
也正确)
解析

练习册系列答案
相关题目
如图在△ 中,
中, ∥
∥ ,
, ,
, 交于点
交于点 ,则图中相似三角形的对数为( ).
,则图中相似三角形的对数为( ).
| A.1 | B.2 | C.3 | D.4 |
如图,锐角三角形ABC的高CD和高BE相交于O,则与△DOB相似的三角形个数是( )
| A.1 | B.2 | C.3 | D.4 |
若一个直角三角形的一条直角边为3 cm,斜边上的高为2.4 cm,则这个直角三角形的面积为
| A.7.2 cm2 | B.6 cm2 |
| C.12 cm2 | D.24 cm2 |
如图所示,若D是 的中点,则与∠ABD相等的角的个数是
的中点,则与∠ABD相等的角的个数是
| A.7 | B.3 |
| C.2 | D.1 |
 中,圆
中,圆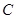 的参数方程为
的参数方程为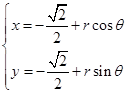 (
(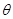 为参数,
为参数,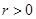 )。以
)。以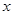 轴正半轴为极轴,并取相同的单位建立极坐标系,直线
轴正半轴为极轴,并取相同的单位建立极坐标系,直线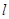 的极坐标方程为
的极坐标方程为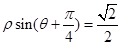 。写出圆心的极坐标,并求当
。写出圆心的极坐标,并求当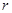 为何值时,圆
为何值时,圆 ,半径r=1,P在圆C上运动。
,半径r=1,P在圆C上运动。 的圆的极坐标方程.
的圆的极坐标方程. 的圆心且与极轴垂直的直线的极坐标方程。
的圆心且与极轴垂直的直线的极坐标方程。