题目内容
已知动点M(x,y)的坐标满足方程
-
=8,则M的轨迹方程是( )
| (x+5)2+y2 |
| (x-5)2+y2 |
A.
| B.
| ||||||||
C.
| D.
|
M设A(-5,0),B(5,0)
由于动点P(x,y)的轨迹方程为
-
=8,
则|MB|-|MA|=8,故点P到定点B(-5,0)与到定点A(5,0)的距离差为8,
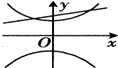
则动点M(x,y)的轨迹是以(±5,0)为焦距,以8为实轴长的双曲线的右支,
由于2a=8,c=5,则b2=c2-a2=25-16=9,
故M的轨迹的标准方程为:
-
=1(x>0).
故选:C.
由于动点P(x,y)的轨迹方程为
| (x+5)2+y2 |
| (x-5)2+y2 |
则|MB|-|MA|=8,故点P到定点B(-5,0)与到定点A(5,0)的距离差为8,
则动点M(x,y)的轨迹是以(±5,0)为焦距,以8为实轴长的双曲线的右支,
由于2a=8,c=5,则b2=c2-a2=25-16=9,
故M的轨迹的标准方程为:
| x2 |
| 16 |
| y2 |
| 9 |
故选:C.

练习册系列答案
相关题目
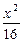 -
-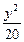 =1的焦点,点P在双曲线上
=1的焦点,点P在双曲线上 若点P到焦点F1的距离等于9,求点P到焦点F2的距离
若点P到焦点F1的距离等于9,求点P到焦点F2的距离