题目内容
（Ⅰ）观察①tan10°tan20°+tan20°tan60°+tan60°tan10°=1②tan5°tan10°+tan10°tan75°+tan75°tan5°=1
由以上两式成立，推广到一般结论，写出你的推论．
（Ⅱ）函数f（x）=-x2+2ax+1-a在区间[0，1]上有最大值2，求实数a的值．
【答案】分析：（I）观察所给的两个等式，发现左边都是两个锐角的正切的乘积形式，一共有三项，且三个角的和为定值：直角，右边的值都为常数1，由此类比推广到一般结论即可．
（II）先求对称轴，比较对称轴和区间的关系，利用开口向下的二次函数离对称轴越近函数值越大来解题即可．
解答：解：（I）观察①、②，可得：
若锐角α，β，γ满足α+β+γ=90°，
则tanαtanβ+tanβtanγ+tanαtanγ=1．
（II）对称轴x=a，
当a＜0时，[0，1]是f（x）的递减区间，f（x）max=f（0）=1-a=2
∴a=-1；
当a＞1时，[0，1]是f（x）的递增区间，f（x）max=f（1）=a=2
∴a=2；
当0≤a≤1时，f（x）max=f（a）=）=a2-a+1=2，
解得a=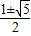
，与0≤a≤1矛盾；
所以a=-1或a=2．
点评：本题主要考查了归纳推理，以及二次函数在闭区间上的最值，同时考查了运算求解的能力，属于基础题．
（II）先求对称轴，比较对称轴和区间的关系，利用开口向下的二次函数离对称轴越近函数值越大来解题即可．
解答：解：（I）观察①、②，可得：
若锐角α，β，γ满足α+β+γ=90°，
则tanαtanβ+tanβtanγ+tanαtanγ=1．
（II）对称轴x=a，
当a＜0时，[0，1]是f（x）的递减区间，f（x）max=f（0）=1-a=2
∴a=-1；
当a＞1时，[0，1]是f（x）的递增区间，f（x）max=f（1）=a=2
∴a=2；
当0≤a≤1时，f（x）max=f（a）=）=a2-a+1=2，
解得a=
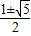，与0≤a≤1矛盾；所以a=-1或a=2．
点评：本题主要考查了归纳推理，以及二次函数在闭区间上的最值，同时考查了运算求解的能力，属于基础题．
练习册系列答案
相关题目