题目内容
设不等式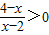
的解集为集合A，关于x的不等式x2+（2a-3）x+a2-3a+2＜0的解集为集合B．（1）若A?B，求实数a的取值范围；
（2）若A∩B=∅，求实数a的取值范围．
【答案】分析：（1）先把不等式
的解集求出来，得到集合A，利用十字分解法求出集合B，再根据子集的定义求出a的范围；
（2）已知A∩B=∅，说明集合A，B没有共同的元素，从而进行求解；
解答：解：由题意，集合
，…（2分）
集合B={x|（x+a-2）（x+a-1）＜0}={x|1-a＜x＜2-a}．…（5分）
（1）若A?B，则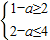
，可得-2≤a≤-1．
所以当-2≤a≤-1时，关系式?B成立．…（8分）
（2）要满足A∩B=∅，应满足2-a≤2或1-a≥4，所以a≥0或a≤-3．
综上所述，a≥0或a≤-3时，A∩B=∅．…（12分）
点评：此题主要考查不等式解集的求法，以及子集的性质，是一道基础题；
的解集求出来，得到集合A，利用十字分解法求出集合B，再根据子集的定义求出a的范围；（2）已知A∩B=∅，说明集合A，B没有共同的元素，从而进行求解；
解答：解：由题意，集合
，…（2分）集合B={x|（x+a-2）（x+a-1）＜0}={x|1-a＜x＜2-a}．…（5分）
（1）若A?B，则
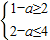，可得-2≤a≤-1．所以当-2≤a≤-1时，关系式?B成立．…（8分）
（2）要满足A∩B=∅，应满足2-a≤2或1-a≥4，所以a≥0或a≤-3．
综上所述，a≥0或a≤-3时，A∩B=∅．…（12分）
点评：此题主要考查不等式解集的求法，以及子集的性质，是一道基础题；
练习册系列答案
相关题目
的解集为集合
，关于
的不等式
的解集为集合
.
，求实数
的取值范围；
，求实数
、
、
都是实数，函数
的导函数为
，
的解集为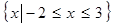
．
的极大值等于
，求
的解集为集合
，当
时，函数
只有一个零点，求实数
的取值范围．
的解集为集合A，关于x的不等式x2+（2a-3）x+a2-3a+2＜0的解集为集合B．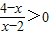
的解集为集合A，关于x的不等式x2+（2a-3）x+a2-3a+2＜0的解集为集合B．