题目内容
设不等式 的解集为集合
的解集为集合 ,关于
,关于 的不等式
的不等式 的解集为集合
的解集为集合 .
.
(I)若 ,求实数
,求实数 的取值范围;
的取值范围;
(II)若 ∩
∩ ,求实数
,求实数 的取值范围.
的取值范围.
【答案】
(I)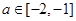 ;(II)
;(II)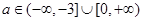 .
.
【解析】
试题分析:由于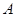 中无参数,先求出集合
中无参数,先求出集合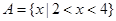 ;再化简第二个不等式,从而解得集合
;再化简第二个不等式,从而解得集合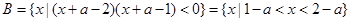 .(I)若
.(I)若 ,则
,则 ,解得
,解得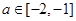 ;(II)若
;(II)若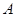 ∩
∩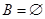 ,则
,则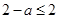 或
或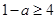 ,解得
,解得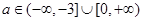 .易错点提示:(1)
.易错点提示:(1)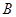 集合是
集合是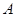 集合的子集,而且
集合的子集,而且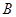 集合中含参数,要注意讨论
集合中含参数,要注意讨论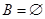 和
和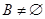 ,此题很明显
,此题很明显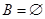 不成立,故不需要讨论;(2)
不成立,故不需要讨论;(2)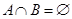 且
且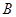 集合中含参数,也要注意讨论
集合中含参数,也要注意讨论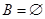 和
和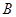 集合与
集合与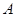 集合没有交叉部分,此题很明显
集合没有交叉部分,此题很明显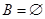 不成立,故不需要讨论.
不成立,故不需要讨论.
试题解析:由题意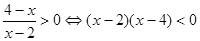 ,解得
,解得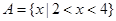 ,集合
,集合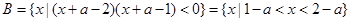
(I)若 ,则
,则 ,解得
,解得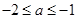 ,即
,即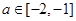 ;
;
(II)若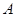 ∩
∩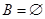 ,则
,则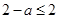 或
或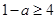 ,解得
,解得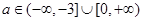 .
.
考点:1.分式不等式与含参一元二次不等式的求解;2.子集的概念理解;3.交集的运算.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 、
、 、
、 都是实数,函数
都是实数,函数 的导函数为
的导函数为 ,
, 的解集为
的解集为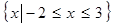 .
. 的极大值等于
的极大值等于 ,求
,求 的解集为集合
的解集为集合 ,当
,当 时,函数
时,函数 只有一个零点,求实数
只有一个零点,求实数 的取值范围.
的取值范围. 的解集为集合A,关于x的不等式x2+(2a-3)x+a2-3a+2<0的解集为集合B.
的解集为集合A,关于x的不等式x2+(2a-3)x+a2-3a+2<0的解集为集合B.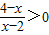 的解集为集合A,关于x的不等式x2+(2a-3)x+a2-3a+2<0的解集为集合B.
的解集为集合A,关于x的不等式x2+(2a-3)x+a2-3a+2<0的解集为集合B.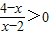 的解集为集合A,关于x的不等式x2+(2a-3)x+a2-3a+2<0的解集为集合B.
的解集为集合A,关于x的不等式x2+(2a-3)x+a2-3a+2<0的解集为集合B.