题目内容
已知函数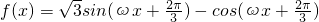 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω的值;
(2)将y=f(x)的图象向右平移 个单位后,得y=g(x)的图象,求g(x)的单调递减区间.
个单位后,得y=g(x)的图象,求g(x)的单调递减区间.
解:(1)因为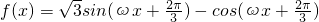
=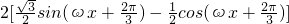
=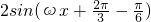 =2cosωx.
=2cosωx.
所以函数的最小正周期为:π,∴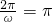 ,ω=2.
,ω=2.
(2)由(1)知f(x)=2cos2x,故 .
.
由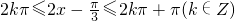 ,解得
,解得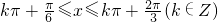 ,
,
即函数g(x)的单调递减区间为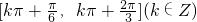 .
.
分析:(1)利用两角和的正弦函数化简函数为一个角的一个三角函数的形式,求出函数的周期即可求ω的值;
(2)利用左加右减的原则,将y=f(x)的图象向右平移 个单位后,得y=g(x)的表达式,通过余弦函数的单调减区间,求g(x)的单调递减区间
个单位后,得y=g(x)的表达式,通过余弦函数的单调减区间,求g(x)的单调递减区间
点评:本题考查三角函数的化简求值,两角和的正弦函数的应用,周期的求法,函数的单调减区间的求法,考查计算能力.
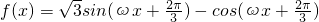
=
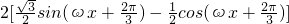
=
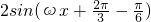 =2cosωx.
=2cosωx.所以函数的最小正周期为:π,∴
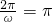 ,ω=2.
,ω=2.(2)由(1)知f(x)=2cos2x,故
 .
.由
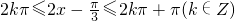 ,解得
,解得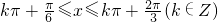 ,
,即函数g(x)的单调递减区间为
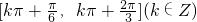 .
.分析:(1)利用两角和的正弦函数化简函数为一个角的一个三角函数的形式,求出函数的周期即可求ω的值;
(2)利用左加右减的原则,将y=f(x)的图象向右平移
 个单位后,得y=g(x)的表达式,通过余弦函数的单调减区间,求g(x)的单调递减区间
个单位后,得y=g(x)的表达式,通过余弦函数的单调减区间,求g(x)的单调递减区间点评:本题考查三角函数的化简求值,两角和的正弦函数的应用,周期的求法,函数的单调减区间的求法,考查计算能力.

练习册系列答案
相关题目
 (-1≤x≤0)的反函数是( )
(-1≤x≤0)的反函数是( )




 的定义域是 ;
的定义域是 ; 上是减函数,则实数a的取值范围是 .
上是减函数,则实数a的取值范围是 .  终边经过点P(-4,3),求
终边经过点P(-4,3),求 的值?
的值? ,(b>0)在
,(b>0)在 的最大值为
的最大值为 ,最小值为-
,最小值为- ,求2a+b的值?
,求2a+b的值?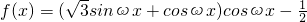 ,(ω>0)的最小正周期为4π.
,(ω>0)的最小正周期为4π. (w>0)的图象的两相邻对称轴间的距离为
(w>0)的图象的两相邻对称轴间的距离为 .
. ,且f(x)=m有且仅有一个实根,求实数m的值.
,且f(x)=m有且仅有一个实根,求实数m的值.