题目内容
已知 分别为椭圆
分别为椭圆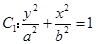 的上、下焦点,
的上、下焦点, 是抛物线
是抛物线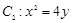 的焦点,点
的焦点,点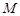 是
是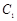 与
与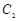 在第二象限的交点, 且
在第二象限的交点, 且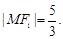
(1)求椭圆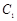 的方程;
的方程;
(2)与圆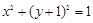 相切的直线
相切的直线 交椭
交椭 于
于 ,若椭圆
,若椭圆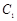 上一点
上一点 满足
满足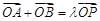 ,求实数
,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2)
解析试题分析:(1)由题意知 ,即
,即 ,利用抛物线定义,可求点
,利用抛物线定义,可求点 的坐标,且
的坐标,且 在椭圆上,利用椭圆的定义可求
在椭圆上,利用椭圆的定义可求 ,从而可求
,从而可求 ,进而确定椭圆
,进而确定椭圆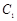 的标准方程;(2)由直线和圆相切的充要条件,得
的标准方程;(2)由直线和圆相切的充要条件,得 ,化简变形为
,化简变形为 ,设
,设 ,结合已知条件,并结合根与系数的关系,将表示点
,结合已知条件,并结合根与系数的关系,将表示点 的坐标用
的坐标用 表示出来,再将点
表示出来,再将点 的坐标代入椭圆方程,得
的坐标代入椭圆方程,得 的方程,同时通过消参,将
的方程,同时通过消参,将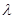 表示为
表示为 的形式,再求其值域即得实数
的形式,再求其值域即得实数 的取值范围.
的取值范围.
(1)由题知 ,所以
,所以 ,
,
又由抛物线定义可知 ,得
,得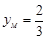 ,
,
于是易知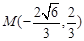 ,从而
,从而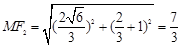 ,
,
由椭圆定义知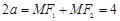 ,得
,得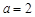 ,故
,故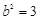 ,
,
从而椭圆的方程为 6分
6分
(2)设 ,则由
,则由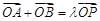 知,
知, ,且
,且 , ①
, ①
又直线 与圆
与圆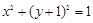 相切,所以有
相切,所以有 ,
,
由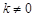 ,可得
,可得 ②
②
又联立 消去
消去 得
得
且 恒成立,且
恒成立,且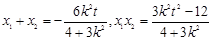 ,
,
所以 ,所以得
,所以得 8分
8分
代入①式得 ,所以
,所以
又将②式代入得,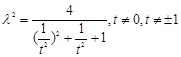 , 10分
, 10分
易知 ,所以
,所以 ,
,
所以 的取值范围为
的取值范围为 13分
13分
考点:1、椭圆的标准方程;2、韦达定理;3、函数的值域.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知 ,
,  , 且
, 且 , 则
, 则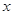 等于 ( )
等于 ( )
| A.-1 | B.-9 | C.9 | D.1 |
四边形 是平行四边形,
是平行四边形, ,
, ,则
,则 = ( )
= ( )
A. | B. | C.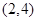 | D.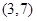 |

 ,并求
,并求 在
在 上的投影
上的投影 ,求
,求 的值,并确定此时它们是同向还是反向?
的值,并确定此时它们是同向还是反向? 中,
中, ,
, 为斜边
为斜边 上靠近顶点
上靠近顶点 的三等分点.
的三等分点. ,求
,求 ;
; ,求
,求 方向上的投影.
方向上的投影.
 的斜坐标定义为:若
的斜坐标定义为:若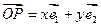 (其中
(其中 、
、 分别为斜坐标系的
分别为斜坐标系的 轴、
轴、 轴正方向上的单位向量,
轴正方向上的单位向量, ),则点
),则点 .在平面斜坐标系
.在平面斜坐标系 中,若
中,若 ,已知点
,已知点 的斜坐标为
的斜坐标为 ,则点
,则点 的距离为 .
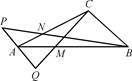
的距离为 .  AC;在AB上取一点M,使得AM=
AC;在AB上取一点M,使得AM= BN;在CM的延长线上取点Q,使得
BN;在CM的延长线上取点Q,使得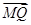 =λ
=λ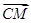 时,
时,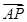 =
=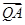 ,试确定λ的值.
,试确定λ的值.