题目内容
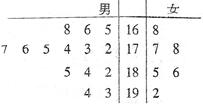
在某次测验中，有6位同学的平均成绩为75分．用
表示编号为
（
）的同学所得成绩，且前5位同学的成绩如下：70,76,72,70,72.
(1)求第6位同学的成绩
，及这6位同学成绩的标准差
；
(2)从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间(68,75)中的概率．
（1）s＝7；（2）
解析试题分析：（1）根据平均数公式写出这组数据的平均数表示式，在表示式中有一个未知量，根据解方程的思想得到结果，求出这组数据的方差，再进一步做出标准差．
（2）本题是一个古典概型，试验发生包含的事件是从5位同学中选2个，共有C52种结果，满足条件的事件是恰有一位成绩在区间（68，75）中，共有C41种结果，根据概率公式得到结果．
试题解析：解：(1)∵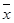
＝75，
∴＝6×75－70－76－72－70－72＝90， 2分
s2＝
(52＋12＋32＋52＋32＋152)＝49，
∴s＝7. 4分
(2)从5位同学中随机选取2位同学，共有如下10种不同的取法：
{1,2}，{1,3}，{1,4}，{1,5}，{2,3}，{2,4}，{2,5}，{3,4}，{3,5}，{4,5}． 8分
选出的2位同学中，恰有1位同学的成绩位于(68,75)的取法共有如下4种：
{1,2}，{2,3}，{2,4}，{2,5}， 10分
故所求概率为. 12分
考点：（1）数字特征；（2）古典概型.
；为缓解某路段交通压力,计划将该路段实施“交通限行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:
| 年龄 (岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频 数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成 人数 | 4 | 8 | 9 | 6 | 4 | 3 |
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
研究性学习小组为了解某生活小区居民用水量
（吨）与气温
（℃）之间的关系，随机统计并制作了5天该小区居民用水量与当天气温的对应表：
| 日期 | 9月5日 | 10月3日 | 10月8日 | 11月16日 | 12月21日 |
| 气温（℃） | 18 | 15 | 11 | 9 | -3 |
| 用水量（吨） | 57 | 46 | 36 | 37 | 24 |
（2）由表中数据求得线性回归方程
中的
，试求出
的值，并预测当地气温为5℃时，该生活小区的用水量. 甲、乙两所学校高三年级分别有1 200人，1 000人，为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：
甲校：
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 8 | 15 |
| | | | | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | x | 3 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| | | | | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
(2)若规定考试成绩在[120,150]内为优秀，请分别估计两所学校数学成绩的优秀率；
(3)由以上统计数据填写下面的2×2列联表，并判断能否在犯错误的概率不超过0.10的前提下认为两所学校的数学成绩有差异.
| | 甲校 | 乙校 | 总计 |
| 优秀 | | | |
| 非优秀 | | | |
| 总计 | | | |
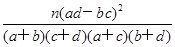. ?临界值表
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
