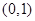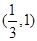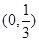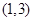题目内容
棱长均为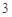 三棱锥
三棱锥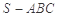 ,若空间一点
,若空间一点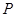 满足
满足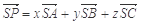
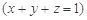 则
则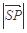 的最小值为( )
的最小值为( )
A.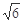 | B.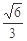 | C.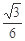 | D.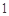 |
A
解析试题分析:根据空间向量基本定理知,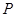 与
与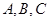 共面,则
共面,则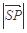 的最小值为三棱锥的高,所以
的最小值为三棱锥的高,所以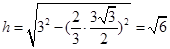 ,故选A.
,故选A.
考点:1.空间向量基本定理;2.正四面体的应用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知向量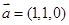 ,
,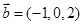 ,且
,且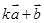 与
与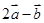 互相垂直,则
互相垂直,则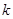 的值是( )
的值是( )
| A.1 | B.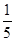 | C.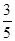 | D.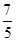 |
已知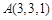 ,
,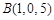 ,则下面说法中,正确的个数是 ( )
,则下面说法中,正确的个数是 ( )
(1)线段AB的中点坐标为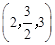 ;(2)线段AB的长度为
;(2)线段AB的长度为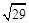 ;
;
(3)到A,B两点的距离相等的点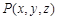 的坐标
的坐标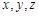 满足
满足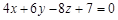 .
.
| A.0个 | B.1个 | C.2个 | D.3个 |
空间直角坐标系中,点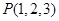 关于
关于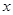 轴对称的点的坐标是( )
轴对称的点的坐标是( )
A.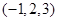 | B.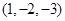 | C.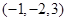 | D.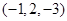 |
在四棱锥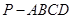 中,
中,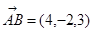 ,
,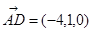 ,
,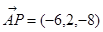 ,则这个四棱锥的高
,则这个四棱锥的高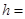
| A.1 | B. 2 | C. 13 | D. 26 |
若向量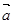 、
、 的坐标满足
的坐标满足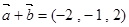 ,
,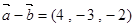 ,则
,则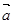 ·
· 等于
等于
A. | B.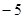 | C.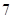 | D.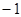 |
若两点的坐标是A(3cosα,3sinα,1),B(2cosβ,2sinβ,1),则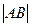 的取值范围是( )
的取值范围是( )
| A.[0,5] |
| B.[1,25] |
| C.(0,5) |
| D.[1,5] |
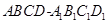 的对角线
的对角线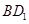 上一点,记
上一点,记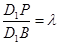 .当
.当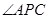 为钝角时,则
为钝角时,则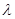 的取值范围为( )
的取值范围为( )