题目内容
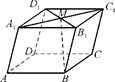
记动点P是棱长为1的正方体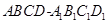 的对角线
的对角线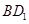 上一点,记
上一点,记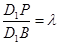 .当
.当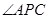 为钝角时,则
为钝角时,则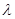 的取值范围为( )
的取值范围为( )
A.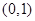 | B.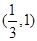 | C.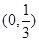 | D.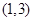 |
B
解析试题分析:由题意可知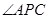 不能为平角,那么则
不能为平角,那么则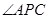 为钝角时,数量积小于零。
为钝角时,数量积小于零。
由题设可知,以DA,DC,DD1,单位正交基底,建立如图所示的空间直角坐标系D-xyz,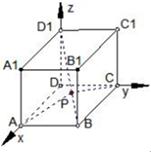
则有A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,1)
由D1B=(1,1,-1),得D1P==λ,D1B=(λ,λ,-λ),所以PA=PD1+D1A=(-λ,-λ,λ)+(1,0,-1)=(1-λ,-λ,λ-1),PC= =(-λ,-λ,λ)+(0,1,-1)=(-λ,1-λ,λ-1)
显然∠APC不是平角,所以∠APC为钝角等价于cos∠APC=cos<PA,PC>= <0等价于
<0等价于
即(1-λ)(-λ)+(-λ)(1-λ)+(λ-1)2=(λ-1)(3λ-1)<0,得 <λ<1因此,λ的取值范围是(
<λ<1因此,λ的取值范围是( ,1),选B。
,1),选B。
考点:本试题主要考查了用空间向量求直线间的夹角,一元二次不等式的解法,属于基础题
点评:解决该试题的关键是建立空间直角坐标系,表示出向量的坐标,运用向量的夹角公式得到参数的范围。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
棱长均为 三棱锥
三棱锥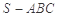 ,若空间一点
,若空间一点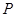 满足
满足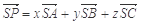
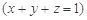 则
则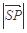 的最小值为( )
的最小值为( )
A.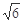 | B.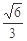 | C.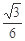 | D.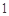 |
若向量a=(1,l,2),b=(2,-1,2),a、b夹角的余弦值为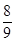 ,则l=( )
,则l=( )
| A.2 | B.-2 | C.-2或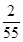 | D.2或-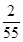 |
若平面α,β垂直,则下面可以是这两个平面的法向量的是( )
| A.n1=(1,2,1),n2=(-3,1,1) |
| B.n1=(1,1,2),n2=(-2,1,1) |
| C.n1=(1,1,1),n2=(-1,2,1) |
| D.n1=(1,2,1),n2=(0,-2,-2) |
若向量a=(1,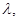 0),b=(2,0,0)且a与b的夹角为
0),b=(2,0,0)且a与b的夹角为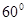 ,则
,则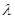 等于
等于
| A.1 | B. |
C.- 或 或 | D.-1或1 |
 ,
,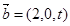 且
且 ,则
,则 的值为
的值为 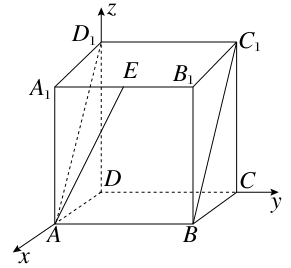
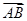 =a,
=a, =b,
=b,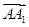 =c,则
=c,则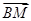 =________.
=________.