题目内容
已知两个定点A、B的坐标分别为(-1,0)和(1,0),动点P满足 (O为坐标原点).
(O为坐标原点).(I)求动点P的轨迹E的方程;
(II)过点C(0,1)的直线l与轨迹E在x轴上方部分交于M、N两点,线段MN的垂直平分线与x轴交于D点,求D点横坐标的取值范围.
【答案】分析:(I)设P(x,y),则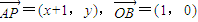 ,
,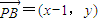 ,由题意知
,由题意知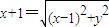 ,所以动点P的轨迹E的方程是y2=4x.
,所以动点P的轨迹E的方程是y2=4x.
(II)设直线l的方程为x=k(y-1),代入轨迹E的方程y2=4x,整理得:y2-4ky+4k=0.由题意知k>1.由根与系数的关系可得MN的中点坐标为(k(2k-1),2k),由此可知线段MN垂直平分线方程为:y-2k=-k[x-k(2k-1)],由此能够求出D点横坐标的取值范围.
解答:解:(I)设P(x,y),则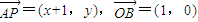 ,
,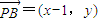 ,
,
∵动点P满足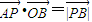 (O为坐标原点),
(O为坐标原点),
∴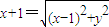 ,整理得y2=4x.
,整理得y2=4x.
∴动点P的轨迹E的方程是y2=4x.
(II)设直线l的方程为x=k(y-1),
代入轨迹E的方程y2=4x,整理得:y2-4ky+4k=0.
由题意知,(4k)2-4×4k>0且4k>0,解得k>1.
由根与系数的关系可得MN的中点坐标为(k(2k-1),2k),
∴线段MN垂直平分线方程为:y-2k=-k[x-k(2k-1)],
令y=0,得D点的横坐标x=2k2-k+2,
∵k>1,
∴x>3,即为所求
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解答.
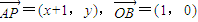 ,
,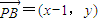 ,由题意知
,由题意知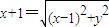 ,所以动点P的轨迹E的方程是y2=4x.
,所以动点P的轨迹E的方程是y2=4x.(II)设直线l的方程为x=k(y-1),代入轨迹E的方程y2=4x,整理得:y2-4ky+4k=0.由题意知k>1.由根与系数的关系可得MN的中点坐标为(k(2k-1),2k),由此可知线段MN垂直平分线方程为:y-2k=-k[x-k(2k-1)],由此能够求出D点横坐标的取值范围.
解答:解:(I)设P(x,y),则
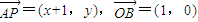 ,
,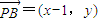 ,
,∵动点P满足
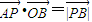 (O为坐标原点),
(O为坐标原点),∴
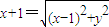 ,整理得y2=4x.
,整理得y2=4x.∴动点P的轨迹E的方程是y2=4x.
(II)设直线l的方程为x=k(y-1),
代入轨迹E的方程y2=4x,整理得:y2-4ky+4k=0.
由题意知,(4k)2-4×4k>0且4k>0,解得k>1.
由根与系数的关系可得MN的中点坐标为(k(2k-1),2k),
∴线段MN垂直平分线方程为:y-2k=-k[x-k(2k-1)],
令y=0,得D点的横坐标x=2k2-k+2,
∵k>1,
∴x>3,即为所求
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细解答.

练习册系列答案
相关题目