题目内容
已知直线: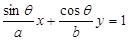 (
( 为给定的正常数,
为给定的正常数,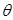 为参数,
为参数,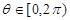 )构成的集合为S,给出下列命题:
)构成的集合为S,给出下列命题:
①当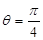 时,
时,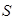 中直线的斜率为
中直线的斜率为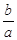 ;
;
②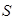 中的所有直线可覆盖整个坐标平面.
中的所有直线可覆盖整个坐标平面.
③当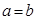 时,存在某个定点,该定点到
时,存在某个定点,该定点到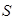 中的所有直线的距离均相等;
中的所有直线的距离均相等;
④当 >
> 时,
时,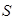 中的两条平行直线间的距离的最小值为
中的两条平行直线间的距离的最小值为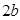 ;
;
其中正确的是 (写出所有正确命题的编号).
③④.
解析试题分析:对于①,当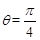 时,
时,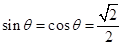 ,
,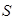 中直线的斜率为-
中直线的斜率为-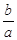 ,故①不正确;对于②,点(0,0)不满足方程,所以S中的所有直线不可覆盖整个平面;对于③,当a=b时,方程为
,故①不正确;对于②,点(0,0)不满足方程,所以S中的所有直线不可覆盖整个平面;对于③,当a=b时,方程为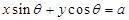 ,
,
存在定点(0,0),该定点到S中的所有直线的距离均相等,均为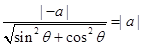 ;对于④,因为
;对于④,因为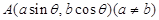 既满足直线
既满足直线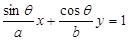 的方程,也满足椭圆
的方程,也满足椭圆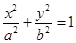 的方程,且把直线
的方程,且把直线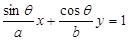 的方程代入椭圆
的方程代入椭圆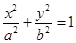 的方程可得
的方程可得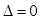 ,当
,当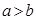 时,
时,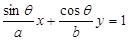 为椭圆的切线,当S中两直线分别与椭圆相切于短轴两端点时,它们间的距离为2b,即为最小距离,故本题选③④.
为椭圆的切线,当S中两直线分别与椭圆相切于短轴两端点时,它们间的距离为2b,即为最小距离,故本题选③④.
考点:直线的斜截式方程,点到线的距离公式,椭圆的标准方程与性质.

练习册系列答案
相关题目
已知直线 与
与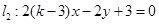 垂直,则
垂直,则 的值是( )
的值是( )
| A.1或3 | B.1或5 | C.1或4 | D.1或2 |
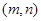 重合,则
重合,则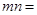 .
. 的斜率为______________________。
的斜率为______________________。 的倾斜角为 .
的倾斜角为 .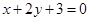 在
在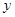 轴上的截距为 ( )
轴上的截距为 ( )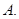
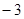
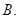
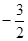
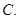
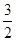
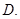
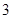
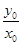 的取值范围为________.
的取值范围为________.