题目内容
用1，2，3，4，5，6组成六位数（没有重复数字），要求任何相邻两个数字的奇偶性不同，且1和2不相邻，这样的六位数的个数是 （用数字作答)。
32
假设偶数在奇数位.
先讨论2 假如2在个位 则1不在十位 排列就是
假如2在百位 则1不可以在十位 也不可以在千位， 则排列是
假如2在万位..和个位一样 是
所以有8+4+4=16种
偶数在偶数位和在奇数为一样
所以总共是16*2=32种.
先讨论2 假如2在个位 则1不在十位 排列就是
假如2在百位 则1不可以在十位 也不可以在千位， 则排列是
假如2在万位..和个位一样 是
所以有8+4+4=16种
偶数在偶数位和在奇数为一样
所以总共是16*2=32种.
练习册系列答案
阅读快车系列答案
相关题目
的解的组数为（ ）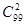
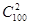
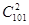
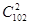
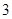位行政领导从初一至初六值班，每天安排
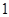人，每人值班两天，则共有多少种安排方案？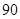
．
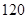
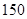
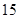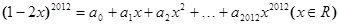，则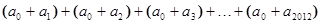
= ▲ ．