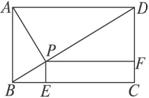
题目内容
 在矩形ABCD中,AB=1,AD=4,E、F分别是AD、BC的中点,以EF为折痕把四边形EFCD折起,当∠CEB=90°时,二面角C-EF-B的平面角的余弦值等于
在矩形ABCD中,AB=1,AD=4,E、F分别是AD、BC的中点,以EF为折痕把四边形EFCD折起,当∠CEB=90°时,二面角C-EF-B的平面角的余弦值等于-
| 1 |
| 4 |
-
.| 1 |
| 4 |
分析:本题为折叠问题,注意到一些长度和角度的不变性,由题意CF⊥EF,BF⊥EF,所以∠CFB即为二面角C-EF-B的平面角,故只需求出BC的长度,而在△CEB中可求得BC,再由余弦定理求解即可.
解答:解:由已知,得出CF⊥EF,BF⊥EF,所以∠CFB 为二面角C-EF-B的平面角.
当∠CEB=90°时,△CEB为等腰直角三角形,CE=BE=
=
,BC=
.
在△CFB中,根据余弦定理得出cos∠CFB=
=
=-
,
故答案为:-
当∠CEB=90°时,△CEB为等腰直角三角形,CE=BE=
| 12+22 |
| 5 |
| 10 |
在△CFB中,根据余弦定理得出cos∠CFB=
| CF2+BF2-BC2 |
| 2CF•BF |
| 4+4-10 |
| 2×2×2 |
| 1 |
| 4 |
故答案为:-
| 1 |
| 4 |
点评:本题考查折叠问题、求二面角、解三角形等知识,考查空间想象能力和运算能力,在折叠问题中注意“变”和“不变”.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3 如图,在矩形ABCD中,已知AD=2,AB=a(a>2),E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积.
如图,在矩形ABCD中,已知AD=2,AB=a(a>2),E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积.