题目内容
若![]() ,
,![]() ,x∈R,p1,p2为常数,且
,x∈R,p1,p2为常数,且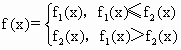
(1)求f(x)=f1(x)对所有实数x成立的充要条件(用p1,p2表示)
(2)设a,b为两实数,a<b且p1,p2∈(a,b)若f(a)=f(b)
求证:f(x)在区间[a,b]上的单调增区间的长度和为![]() (闭区间[m,n]的长度定义为n-m)
(闭区间[m,n]的长度定义为n-m)
答案:
解析:
解析:
|
本小题考查充要条件、指数函数于绝对值函数、不等式的综合运用. (1) 若 当 所以 当 所以 综上所述, (2)10如果 因为 因为减区间为 20如果 于是当 当 当 由方程 显然 所以 综上可知,在区间 故由函数 故由(1)(2)得 综合1020可知,
|

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
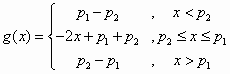
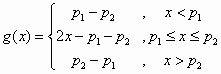
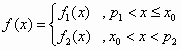
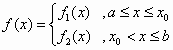 (如图2)
(如图2)
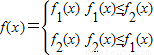
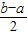 .(区间[m,n]、(m,n)或(m,n]的长度均定义为n-m)
.(区间[m,n]、(m,n)或(m,n]的长度均定义为n-m)