题目内容
设二次函数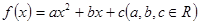 满足下列条件:①当
满足下列条件:①当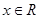 时,
时,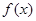 的最小值为
的最小值为 ,且图像关于直线
,且图像关于直线 对称;②当
对称;②当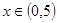 时,
时,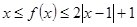 恒成立.
恒成立.
(1)求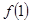 的值;
的值;
(2)求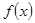 的解析式;
的解析式;
(3)若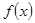 在区间
在区间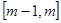 上恒有
上恒有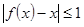 ,求实数
,求实数 的取值范围.
的取值范围.
【答案】
(1)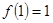 (2)
(2)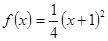 (3)
(3)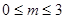
【解析】
试题分析:(1)在②中令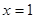 ,有
,有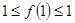 ,故
,故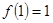 . 4分
. 4分
(2)当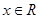 时,
时,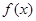 的最小值为
的最小值为 且二次函数关于直线
且二次函数关于直线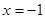 对称,
对称,
故设此二次函数为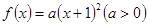 .
6分
.
6分
因为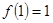 ,得
,得 . 8分
. 8分
所以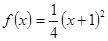 . 10分
. 10分
(3)记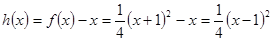 ,
,
显然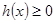 ,
, 在区间
在区间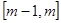 上恒有
上恒有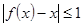 ,即
,即 , 12分
, 12分
令 ,得
,得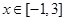 ,由
,由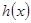 的图像只须
的图像只须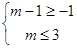 ,
15分
,
15分
解得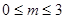 . 16分
. 16分
考点:本小题主要考查二次函数的图象和性质及恒成立问题.
点评:二次函数是高中学习中比较重要的一类函数,要准确掌握,灵活求解;恒成立问题一般转化为最值问题解决,这是经常考查的题型.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
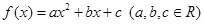 满足下列条件:
满足下列条件: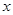 ∈R时,
∈R时,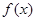 的最小值为0,且f (
的最小值为0,且f (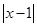 +1恒成立。
+1恒成立。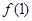 的值;
的值; 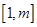 时,就有
时,就有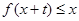 成立。
成立。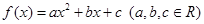 满足下列条件:
满足下列条件: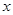 ∈R时,
∈R时,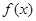 的最小值为0,且f (
的最小值为0,且f (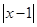 +1恒成立。
+1恒成立。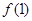 的值;
的值; 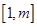 时,就有
时,就有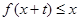 成立。
成立。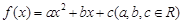 满足下列条件:
满足下列条件: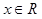 时,其最小值为0,且
时,其最小值为0,且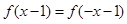 成立;
成立;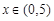 时,
时,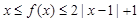 恒成立.
恒成立.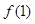 的值;
的值;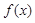 的解析式;
的解析式;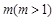 ,使得存在
,使得存在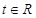 ,只要当
,只要当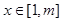 时,就有
时,就有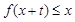 成立
成立