题目内容
已知复数z是关于x的实系数一元二次方程x2+mx+25=0的一个根,同时复数z满足关系式|z|+z=8+4i.
(1)求|z|的值及复数z;
(2)求实数m的值.
解:(1)设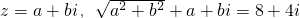
则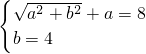
得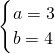
所以:z=3+4i,|z|=5
(2)因为方程两根之积为25,所以 也是原方程的一根,且
也是原方程的一根,且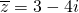
所以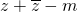
故:m=-6.
分析:(1)直接设出复数z,利用复数相等对应实部和实部相等,虚部和虚部相等解方程即可求出|z|的值及复数z;
(2)因为方程两根之积为25,所以 也是原方程的一根,再结合(1)的结论和一元二次方程的根的分布与系数的关系即可求出实数m的值.
也是原方程的一根,再结合(1)的结论和一元二次方程的根的分布与系数的关系即可求出实数m的值.
点评:本题第一问中涉及到复数相等.复数相等的对应结论是实部和实部相等,虚部和虚部相等.
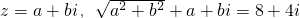
则
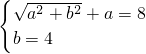
得
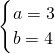
所以:z=3+4i,|z|=5
(2)因为方程两根之积为25,所以
 也是原方程的一根,且
也是原方程的一根,且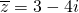
所以
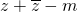
故:m=-6.
分析:(1)直接设出复数z,利用复数相等对应实部和实部相等,虚部和虚部相等解方程即可求出|z|的值及复数z;
(2)因为方程两根之积为25,所以
 也是原方程的一根,再结合(1)的结论和一元二次方程的根的分布与系数的关系即可求出实数m的值.
也是原方程的一根,再结合(1)的结论和一元二次方程的根的分布与系数的关系即可求出实数m的值.点评:本题第一问中涉及到复数相等.复数相等的对应结论是实部和实部相等,虚部和虚部相等.

练习册系列答案
相关题目
已知复数z=-3+2i(i为虚数单位)是关于x的方程2x2+px+q=0(p,q为实数)的一个根,则p+q的值为( )
| A、22 | B、36 | C、38 | D、42 |
 .
.