题目内容
15、给出下列命题:
①不存在实数a,b使f(x)=lg(x2+ax+b)的定义域、值域均为一切实数;
②函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称;
③方程ln x+x=4有且只有一个实数根;
④a=-1是方程a2x2+(a+2)y2+2ax+a=0表示圆的充分必要条件
⑤过椭圆右焦点的直线与椭圆交于A,B两点,则以AB为直径的圆与其右准线相离其中真命题的序号是
①不存在实数a,b使f(x)=lg(x2+ax+b)的定义域、值域均为一切实数;
②函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称;
③方程ln x+x=4有且只有一个实数根;
④a=-1是方程a2x2+(a+2)y2+2ax+a=0表示圆的充分必要条件
⑤过椭圆右焦点的直线与椭圆交于A,B两点,则以AB为直径的圆与其右准线相离其中真命题的序号是
②、⑤
.(写出所有真命题的序号)分析:根据对数函数的值域与定义域,可以判断①的真假;根据函数图象的对称变换法则,我们可以判断②的真假;根据函数零点个数与对应方程根的个数之间的关系,可以判断③的真假;利用圆的方程的特点,我们可以判断④的对错;根据椭圆的几何特征,我们可以判断⑤的真假;进而得到答案.
解答:解:若函数f(x)=lg(x2+ax+b)的定义域为R,则x2+ax+b的最小值A大于0,则函数的值域为[lgA,+∞)≠R,故①为假命题;
函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称,故②为真命题;
由于函数y=ln x与函数y=-x+4的图象有且只有一个交点,故③方程ln x+x=4有且只有一个实数根为真命题;
a=-1或a=2是方程a2x2+(a+2)y2+2ax+a=0表示圆的充分必要条件,故④为假命题;
过椭圆右焦点的直线与椭圆交于A,B两点,则以AB为直径的圆与其右准线相离,故⑤为真命题;
故答案为:②、⑤
函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称,故②为真命题;
由于函数y=ln x与函数y=-x+4的图象有且只有一个交点,故③方程ln x+x=4有且只有一个实数根为真命题;
a=-1或a=2是方程a2x2+(a+2)y2+2ax+a=0表示圆的充分必要条件,故④为假命题;
过椭圆右焦点的直线与椭圆交于A,B两点,则以AB为直径的圆与其右准线相离,故⑤为真命题;
故答案为:②、⑤
点评:本题考查的知识点是命题真假判断,其中熟练掌握对数函数的性质,函数图象的对称变换法则,函数零点与对应方程根的关系,圆及椭圆的几何特征是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
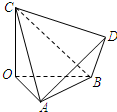 如图,四面体OABC的三条棱OA,OB,OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题.
如图,四面体OABC的三条棱OA,OB,OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题. 如图,四面体OABC的三条棱OA、OB、OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题.
如图,四面体OABC的三条棱OA、OB、OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题.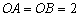 ,
,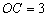 ,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )
,D为四面体OABC外一点.给出下列命题:①不存在点D,使四面体ABCD有三个面是直角三角形;②不存在点D,使四面体ABCD是正三棱锥;③存在点D,使CD与AB垂直并相等;④存在无数个点D,使点O在四面体ABCD的外接球面上.则其中正确命题的序号是( )