题目内容
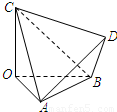
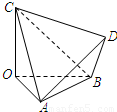
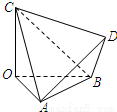
 如图,四面体OABC的三条棱OA、OB、OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题.
如图,四面体OABC的三条棱OA、OB、OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题.①不存在点D,使四面体ABCD有三个面是直角三角形
②不存在点D,使四面体ABCD是正三棱锥
③存在点D,使CD与AB垂直并且相等
④存在无数个点D,使点O在四面体ABCD的外接球面上
其中真命题的序号是
③④
③④
.分析:对于①可构造四棱锥CABD与四面体OABC一样进行判定;
对于②,使AB=AD=BD,此时存在点D,使四面体ABCD是正三棱锥;
对于③取CD=AB,AD=BD,此时CD垂直面ABD,即存在点D,使CD与AB垂直并且相等;
对于④先找到四面体OABC的内接球的球心P,使半径为r,只需PD=r,可判定④的真假.
对于②,使AB=AD=BD,此时存在点D,使四面体ABCD是正三棱锥;
对于③取CD=AB,AD=BD,此时CD垂直面ABD,即存在点D,使CD与AB垂直并且相等;
对于④先找到四面体OABC的内接球的球心P,使半径为r,只需PD=r,可判定④的真假.
解答:解:对于①,∵四面体OABC的三条棱OA,OB,OC两两垂直,OA=OB=2,OC=3,
∴AC=BC=
,AB=2
当四棱锥CABD与四面体OABC一样时,即取CD=3,AD=BD=2,四面体ABCD的三条棱DA、DB、DC两两垂直,
此时点D,使四面体ABCD有三个面是直角三角形,故①不正确;
对于②,由①知AC=BC=
,AB=2
,
使AB=AD=BD,此时存在点D,CD=
,使四面体C-ABD是正三棱锥,故②不正确;
对于③,取CD=AB,AD=BD,此时CD垂直面ABD,即存在点D,使CD与AB垂直并且相等,故③正确;
对于④,先找到四面体OABC的内接球的球心P,使半径为r,只需PD=r即可
∴存在无数个点D,使点O在四面体ABCD的外接球面上,故④正确
故答案为:③④.
∴AC=BC=
| 13 |
| 2 |
当四棱锥CABD与四面体OABC一样时,即取CD=3,AD=BD=2,四面体ABCD的三条棱DA、DB、DC两两垂直,
此时点D,使四面体ABCD有三个面是直角三角形,故①不正确;
对于②,由①知AC=BC=
| 13 |
| 2 |
使AB=AD=BD,此时存在点D,CD=
| 13 |
对于③,取CD=AB,AD=BD,此时CD垂直面ABD,即存在点D,使CD与AB垂直并且相等,故③正确;

对于④,先找到四面体OABC的内接球的球心P,使半径为r,只需PD=r即可
∴存在无数个点D,使点O在四面体ABCD的外接球面上,故④正确
故答案为:③④.
点评:本题主要考查了棱锥的结构特征,同时考查了空间想象能力,转化与划归的思想,以及构造法的运用,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
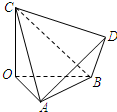 如图,四面体OABC的三条棱OA,OB,OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题.
如图,四面体OABC的三条棱OA,OB,OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题.