题目内容
已知奇函数 f (x) 在 (-¥,0)∪(0,+¥) 上有意义,且在 (0,+¥) 上是增函数,f (1) = 0,又函数 g(q) = sin 2q+ m cos q-2m,若集合M =" {m" | g(q) < 0},集合 N =" {m" | f [g(q)] < 0},求M∩N.
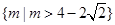 .
.
解析试题分析:根据条件中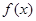 是奇函数的这一条件可以求得使
是奇函数的这一条件可以求得使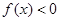 的
的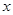 的范围,再根据
的范围,再根据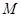 与
与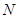 的表达式,可以得到
的表达式,可以得到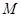 与
与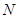 的交集即是使
的交集即是使 恒成立的所有
恒成立的所有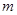 的全体,通过参变分离可以将问题转化为求使
的全体,通过参变分离可以将问题转化为求使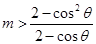 恒成立的
恒成立的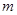 的取值范围,通过求函数最大值,进而可以求出
的取值范围,通过求函数最大值,进而可以求出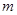 的范围.
的范围.
依题意,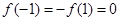 ,又
,又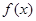 在
在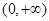 上是增函数,
上是增函数,
∴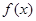 在
在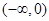 上也是增函数, 1分
上也是增函数, 1分
∴ 由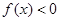 得
得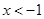 或
或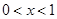 2分
2分
∴ 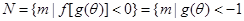 或
或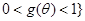 3分
3分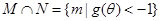 4分
4分
由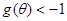 得
得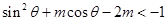 5分
5分
即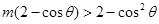 6分
6分
∴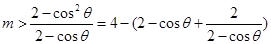 7分
7分
设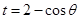 ,
,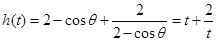 9分
9分
∵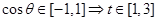 , 10分
, 10分
∴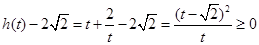 , 11分
, 11分
且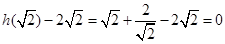 12分
12分
∴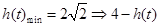 的最大值为
的最大值为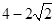 13分
13分
∴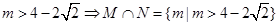 14分
14分
另解:本题也可用下面解法:
1. 用单调性定义证明单调性
∵对任意 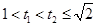 ,
,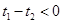 ,
,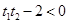 ,
,
∴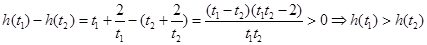 ,
,
即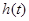 在
在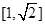 上为减函数,
上为减函数,
同理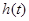 在
在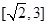 上为增函数,得
上为增函数,得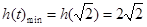 5分
5分
∴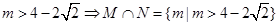 .
.
2. 二次函数最值讨论
解:依题意,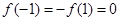 ,又
,又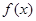 在
在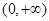 上是增函数,
上是增函数,
∴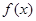 在
在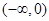

练习册系列答案
相关题目
 有最小正周期2,且当
有最小正周期2,且当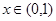 时,
时, .
.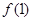 和
和 的值;
的值; 在(0,1]上解的个数.
在(0,1]上解的个数.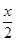 +
+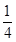 .
.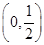 ,使f(x0)=x0.
,使f(x0)=x0.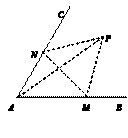
 中,
中, 为奇数,
为奇数, 均为整数,且
均为整数,且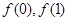 均为奇数.求证:
均为奇数.求证: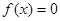 无整数根。
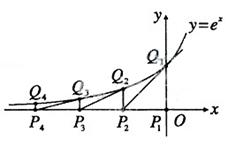
无整数根。 轴的垂线交曲线
轴的垂线交曲线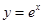 于点
于点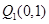 ,曲线在
,曲线在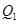 点处的切线与
点处的切线与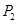 .再从
.再从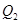 ,依次重复上述过程得到一系列点:
,依次重复上述过程得到一系列点: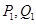 ;
;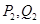 ;…;
;…; ,记
,记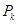 点的坐标为
点的坐标为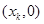 (
(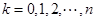 ).
).
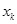 与
与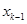 的关系(
的关系(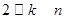 );
);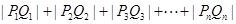 .
. km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
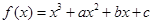 在
在 与
与 时都取得极值.
时都取得极值. 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.