Question

已知f(x)＝ln(ax＋b)－x其中a＞0，b＞0．

(Ⅰ)求使f(x)在[0，＋∞)上是减函数的充要条件；

(Ⅱ)求f(x)在[0，＋∞)上的最大值．

Answer 1

答案：
解析：

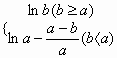(Ⅰ)∵　　2分 　　∵x≥0，a＞0，b＞0　∴≤0，a－b≤0　即a≤b　　4分 　　当a≤b时　∵a＞0，b＞0，x≥0　∴ax＋b＞0，a－b－ax≤0即≤0 　　∴在[0，＋∞)上是减函数的充要条件为b≥a　　6分 　　(Ⅱ)由(Ⅰ)知：当b≥a时，在[0，＋∞)上是减函数，∴最大值＝＝lnb　　8分 　　当b＜a时，∵＝ 　　∴当0≤x＜时，＞0，当x＞时＜0 　　即在[0，)上是增函数，在[，＋∞)上是减函数，　　10分 　　∴最大值＝()＝lna－　　11分 　　∴最大值＝　　12分