题目内容
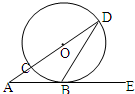
已知：如图，CD是⊙O的直径，AE切⊙O于点B，DC的延长线交AB于点A，∠A=20°，则∠DBE=
55°
55°
．分析：做出辅助线连接BC，由CD是⊙O的直径知道∠CBD=90°，由AE是⊙O的切线知道∠DBE=∠1，∠2=∠D，又∠1+∠D=90°，即∠1+∠2=90°；而∠A+∠2=∠1，由此即可求出∠1，即求出∠DBE．
解答：解：连接BC，
∵CD是⊙O的直径，
∴∠CBD=90°，
∵AE是⊙O的切线，
∴∠DBE=∠1，∠2=∠D；
又∵∠1+∠D=90°，
即∠1+∠2=90°---（1），
∠A+∠2=∠1----（2），
（1）-（2）得∠1=55°
即∠DBE=55°．
故答案为：∠DBE=55°．
∵CD是⊙O的直径，
∴∠CBD=90°，
∵AE是⊙O的切线，
∴∠DBE=∠1，∠2=∠D；
又∵∠1+∠D=90°，
即∠1+∠2=90°---（1），
∠A+∠2=∠1----（2），
（1）-（2）得∠1=55°
即∠DBE=55°．
故答案为：∠DBE=55°．
点评：本题考查的是弦切角的性质及圆周角定理，三角形内角与外角的关系，本题解题的关键是角之间的变换与运算，是一道较简单的题目．
练习册系列答案
相关题目
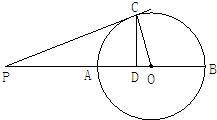已知：如图，AB是⊙O的直径，点C是⊙O上一点，CD⊥AB，垂足为D，点P在BA的延长线上，且PC是圆O的切线．
已知：如图，CD是⊙O的直径，AE切⊙O于点B，DC的延长线交AB于点A，∠A=20°，则
