题目内容
已知y=loga(2-ax)在(0,1)上是增函数,则不等式loga|x+1|>loga|x-3|的解集为 ( )
| A.{x|x<-1} | B.{x|x<1} |
| C.{x|x<1,且x≠-1} | D.{x|x>1} |
C
解析【解题指南】先由对数函数的单调性判断a的范围,再解不等式.
解:选C.因为y=loga(2-ax)在(0,1)上是增函数,
又a>0,所以u=2-ax为减函数,所以0<a<1,
所以|x+1|<|x-3|,且x+1≠0,x-3≠0,
由|x+1|<|x-3|得(x+1)2<(x-3)2,解得x<1.
综上,得x<1且x≠-1.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
某公司利用A、B两种原料生产甲、乙两种产品,每生产1吨产品所需要的原料及利润如下表所示:
| | A种原料(单位:吨) | B种原料(单位:吨) | 利润(单位:万元) |
| 甲种产品 | 1 | 2 | 3 |
| 乙种产品 | 2 | 1 | 4 |
设a,b,c∈R+,且a+b+c=1,若M=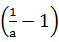 ·
·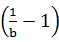 ·
·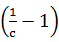 ,则必有 ( )
,则必有 ( )
A.0≤M< | B. ≤M<1 ≤M<1 |
| C.1≤M<8 | D.M≥8 |
已知△ABC中,∠C=90°,则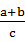 的取值范围是 ( )
的取值范围是 ( )
| A.(0,2) | B.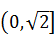 |
C.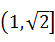 | D.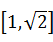 |
在等比数列{an}和等差数列{bn}中,a1=b1>0,a3=b3>0,a1≠a3,则a5与b5的大小关系为 ( )
| A.a5>b5 | B.a5<b5 |
| C.a5=b5 | D.不确定 |
若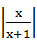 >
>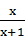 ,则实数x的取值范围是 ( )
,则实数x的取值范围是 ( )
| A.(-1,0) | B.[-1,0] |
| C.(-∞,-1)∪(0,+∞) | D.(-∞,-1]∪[0,+∞) |
下列函数中,最小值是2的是( )
A.y= + + |
B.y=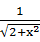 + +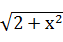 |
C.y=tanx+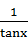 ,x∈ ,x∈ |
D.y=lg(x-10)+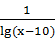 (x>10且x≠11) (x>10且x≠11) |
已知圆柱的轴截面周长为6,体积为V,则下列总成立的是 ( )
| A.V≥π | B.V≤π |
C.V≥ π π | D.V≤ π π |
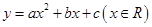 的部分对应值如下表:
的部分对应值如下表:
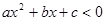 的解集是_______________________.
的解集是_______________________.