题目内容
某公司利用A、B两种原料生产甲、乙两种产品,每生产1吨产品所需要的原料及利润如下表所示:
| | A种原料(单位:吨) | B种原料(单位:吨) | 利润(单位:万元) |
| 甲种产品 | 1 | 2 | 3 |
| 乙种产品 | 2 | 1 | 4 |
公司每天生产甲、乙两种产品都是 吨时,公司可获得最大利润,最大利润为
吨时,公司可获得最大利润,最大利润为 万元.
万元.
解析试题分析:解:设生产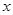 吨甲种产品,
吨甲种产品, 吨乙种产品,总利润为Z(万元),
吨乙种产品,总利润为Z(万元),
则约束条件为 , 4分
, 4分
目标函数为 , 5分
, 5分
可行域为下图中的阴影部分: 9分
9分
化目标函数为斜截式方程: 
当目标函数直线经过图中的点M时, 有最大值, 10分
有最大值, 10分
联立方程组 ,
,
解得 , 所以
, 所以 , 12分
, 12分
将 代入目标函数得
代入目标函数得 (万元).
(万元).
答:公司每天生产甲、乙两种产品都是 吨时,公司可获得最大利润,最大利润为
吨时,公司可获得最大利润,最大利润为 万元.
万元.
14分
考点:线性规划的运用
点评:主要是考查了线性规划的最优解的运用,属于中档题。

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大。已知对这两种产品有直接限制的因素是资金和劳动力,经调查,得到关于这两种产品的有关数据如下表:
| 资 金 | 每台单位产品所需资金(百元) | 月资金供应量 (百元) | |
| 空调机 | 洗衣机 | ||
| 成 本 | 30 | 20 | 300 |
| 劳动力(工资) | 5 | 10 | 110 |
| 每台产品利润 | 6 | 8 | |
已知不等式 恒成立,则实数m的取值范围是( )
恒成立,则实数m的取值范围是( )
A. | B. |
C. 或 或 | D. 或 或 |
用反证法证明命题“ ”,其反设正确的是( )
”,其反设正确的是( )
A.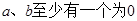 | B. |
C. | D. |
已知y=loga(2-ax)在(0,1)上是增函数,则不等式loga|x+1|>loga|x-3|的解集为 ( )
| A.{x|x<-1} | B.{x|x<1} |
| C.{x|x<1,且x≠-1} | D.{x|x>1} |
不等式x2﹣4x+a<0存在小于1的实数解,则实数a的取值范围是( )
| A.(﹣∞,4) | B.(﹣∞,4] |
| C.(﹣∞,3) | D.(﹣∞,3] |
 满足
满足 ,则
,则 的最小值是__________.
的最小值是__________.