题目内容
(本题满分12 分)
已知数列 为等比数列,且首项为
为等比数列,且首项为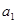 ,公比为
,公比为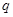 ,前
,前 项和为
项和为 .
.
(Ⅰ)试用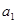 ,
,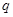 ,
, 表示前
表示前 项和
项和 ;
;
(Ⅱ)证明(Ⅰ)中所写出的等比数列的前 项和公式。
项和公式。
(Ⅰ)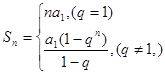 (Ⅱ)见解析
(Ⅱ)见解析
解析试题分析:(Ⅰ)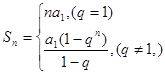 …4分
…4分
(Ⅱ)证明:当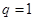 时,
时,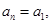 所以
所以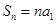 ;
;
当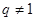 时,
时,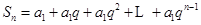 ,(1)
,(1)
所以 ,(2)
,(2)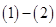 得:
得: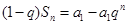 ,所以
,所以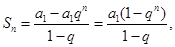
综上所述,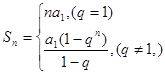 . …12分
. …12分
考点:本小题主要考查等比数列的前 项和公式及其公式的推导过程,考查学生的逻辑推理能力和论证能力.
项和公式及其公式的推导过程,考查学生的逻辑推理能力和论证能力.
点评:推导等比数列的前 项和公式的方法是“错位相减法”,这种方法在数列求和中经常用到,但是由于往往运算量比较大,很多学生出错,所以要多加练习,熟能生巧.
项和公式的方法是“错位相减法”,这种方法在数列求和中经常用到,但是由于往往运算量比较大,很多学生出错,所以要多加练习,熟能生巧.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
已知函数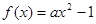 的图像在点A(1,f(1))处的切线
的图像在点A(1,f(1))处的切线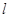 与直线
与直线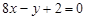 平行,若数列
平行,若数列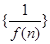 的前
的前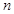 项和为
项和为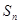 ,则
,则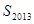 的值为( )
的值为( )
A.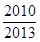 | B.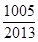 | C.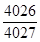 | D.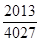 |
 中,
中, ,公比
,公比 .
. 为
为
 ,求数列
,求数列 的通项公式.
的通项公式.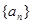 是公差不为零的等差数列,
是公差不为零的等差数列, 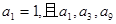 成等比数列.
成等比数列.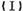 求数列
求数列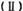 求数列
求数列 的前n项和
的前n项和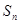
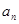 }的前n 项和为
}的前n 项和为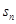 ,已知
,已知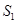 ,
,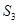 ,
,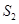 成等差数列
成等差数列 -
-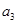 =3,求
=3,求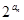 +2n,求数列{bn}的前n项和Tn.
+2n,求数列{bn}的前n项和Tn. 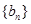 满足
满足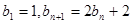 ,
,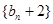 为等比数列 (2)求数列
为等比数列 (2)求数列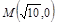 作直线
作直线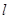 交曲线
交曲线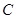 :
: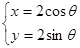 (
(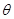 为参数)于
为参数)于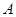 、
、 两点,若
两点,若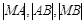 成等比数列,求直线
成等比数列,求直线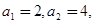 数列
数列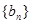 满足:
满足: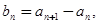
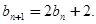
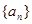 的通项公式.
的通项公式.