题目内容
一个退休职工每年获得一份退休金,金额与他服务的年数的平方根成正比,如果多服务a年,他的退休金会比原来的多p元,如果他多服务b年(b≠a),他的退休金会比原来的多q元,那么他每年的退休金是(用a,b,p,q表示) .
【答案】分析:如果设正常工作x年,退休金与服务年数的平方根的比例系数为k,则k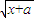 -k
-k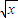 =p①,k
=p①,k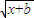 -k
-k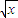 =q②;
=q②;
那么,正常退休时每年的退休金应为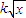 ,不妨设
,不妨设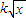 =t,则
=t,则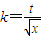 ,①式可化为
,①式可化为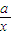 =
=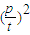 +2
+2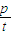 =
=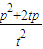 ,
,
②式可化为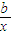 =
=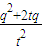 ;两式相比,得出t,即为所求.
;两式相比,得出t,即为所求.
解答:解:设正常工作x年,退休金与服务年数的平方根的比例系数为k,则由题意,得
k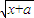 -k
-k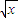 =p①,k
=p①,k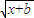 -k
-k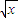 =q②;设
=q②;设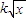 =t,则
=t,则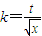 ,①式可化为
,①式可化为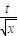 •
•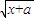 -t=p,即
-t=p,即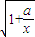 -1=
-1=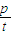 ,∴
,∴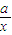 =
=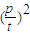 +2
+2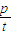 =
=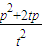 ③;
③;
同理,②式可化为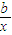 =
=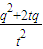 ④;
④;
③÷④,得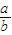 =
=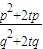 ,∴t=
,∴t=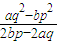 ;所以,正常退休时每年的退休金为
;所以,正常退休时每年的退休金为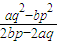 (元).
(元).
故答案为: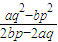 .
.
点评:本题考查了含有二次根式的函数模型的应用,重点是考查了二次根式的运算能力,是中档题.
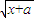 -k
-k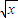 =p①,k
=p①,k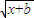 -k
-k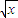 =q②;
=q②;那么,正常退休时每年的退休金应为
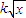 ,不妨设
,不妨设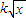 =t,则
=t,则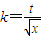 ,①式可化为
,①式可化为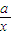 =
=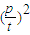 +2
+2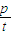 =
=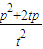 ,
,②式可化为
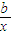 =
=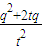 ;两式相比,得出t,即为所求.
;两式相比,得出t,即为所求.解答:解:设正常工作x年,退休金与服务年数的平方根的比例系数为k,则由题意,得
k
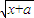 -k
-k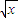 =p①,k
=p①,k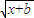 -k
-k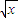 =q②;设
=q②;设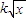 =t,则
=t,则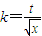 ,①式可化为
,①式可化为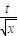 •
•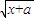 -t=p,即
-t=p,即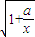 -1=
-1=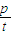 ,∴
,∴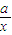 =
=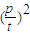 +2
+2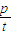 =
=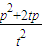 ③;
③;同理,②式可化为
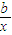 =
=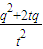 ④;
④;③÷④,得
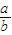 =
=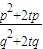 ,∴t=
,∴t=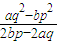 ;所以,正常退休时每年的退休金为
;所以,正常退休时每年的退休金为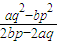 (元).
(元).故答案为:
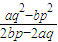 .
.点评:本题考查了含有二次根式的函数模型的应用,重点是考查了二次根式的运算能力,是中档题.

练习册系列答案
相关题目