题目内容
已知函数 .
.
(Ⅰ)求 的最大值,并求出此时
的最大值,并求出此时 的值;
的值;
(Ⅱ)写出 的单调区间.
的单调区间.
 .
.(Ⅰ)求
 的最大值,并求出此时
的最大值,并求出此时 的值;
的值;(Ⅱ)写出
 的单调区间.
的单调区间.解:(Ⅰ)


所以 的最大值为
的最大值为 ,此时
,此时 .………………………3分
.………………………3分
(Ⅱ)由 得
得 ;
;
所以 单调增区间为:
单调增区间为: ;
;
由 得
得
所以 单调减区间为:
单调减区间为: 。………………………6分
。………………………6分



所以
 的最大值为
的最大值为 ,此时
,此时 .………………………3分
.………………………3分(Ⅱ)由
 得
得 ;
;所以
 单调增区间为:
单调增区间为: ;
;由
 得
得
所以
 单调减区间为:
单调减区间为: 。………………………6分
。………………………6分本试题主要是考查了三角函数的图像与性质的运用。
(1)先化简为单一三角函数,然后利用函数的性质得到最值。
(2)利用三角函数的性质得到单调区间,进而得到结论。
(1)先化简为单一三角函数,然后利用函数的性质得到最值。
(2)利用三角函数的性质得到单调区间,进而得到结论。

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
 ,有下列命题:
,有下列命题: ,且
,且 ;
;  对称;
对称;  求得 。
求得 。 作怎样的变换可得到函数
作怎样的变换可得到函数 ( )
( ) 个单位
个单位  个单位
个单位  )图象可以看作把函数y=3sin2x的图象作下列移动而得到( )
)图象可以看作把函数y=3sin2x的图象作下列移动而得到( ) 单位
单位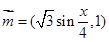 ,
, ,
,
 ,求
,求 的值;
的值; 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求函数
,求函数 的取值范围.
的取值范围. ,
, )
) , π)
, π) ,
, )
) , 2π)
, 2π) 的最小正周期为
的最小正周期为 




 ,
, ,那么
,那么 = ( )
= ( ) 



 的图象的一条对称轴是( )
的图象的一条对称轴是( )


