题目内容
已知数列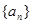 的前
的前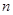 项和为
项和为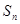 ,数列
,数列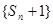 是公比为
是公比为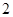 的等比数列,
的等比数列,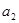 是
是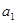 和
和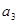 的等比中项.
的等比中项.
(1)求数列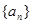 的通项公式;
的通项公式;
(2)求数列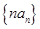 的前
的前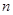 项和
项和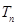 .
.
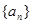 的前
的前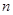 项和为
项和为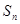 ,数列
,数列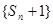 是公比为
是公比为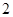 的等比数列,
的等比数列,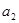 是
是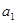 和
和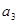 的等比中项.
的等比中项.(1)求数列
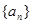 的通项公式;
的通项公式;(2)求数列
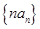 的前
的前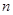 项和
项和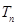 .
.(1)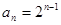 ;(2)
;(2)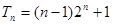 .
.
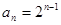 ;(2)
;(2)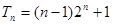 .
.试题分析:(1)先根据等比数列公式求出
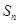 与
与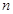 的关系式,然后利用
的关系式,然后利用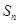 与
与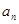 的递推关系求出
的递推关系求出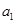 ,从而再求出
,从而再求出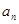 .(2)根据数列通项公式的特点用错位相减法求数列前
.(2)根据数列通项公式的特点用错位相减法求数列前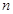 项和.
项和.试题解析:(1)解:∵
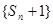 是公比为
是公比为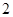 的等比数列,
的等比数列,∴
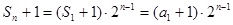 . 1分
. 1分∴
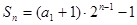 .
. 从而
 ,
,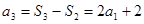 . 3分
. 3分∵
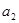 是
是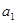 和
和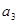 的等比中项
的等比中项∴
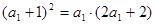 ,解得
,解得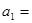
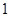 或
或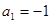 . 4分
. 4分当
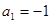 时,
时,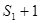
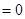 ,
,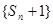 不是等比数列, 5分
不是等比数列, 5分∴
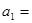
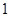 .
.∴
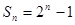 . 6分
. 6分当
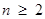 时,
时,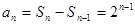 . 7分
. 7分∵
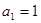 符合
符合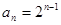 ,
,∴
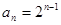 . 8分
. 8分(2)解:∵
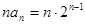 ,
,∴
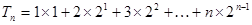 . ① 9分
. ① 9分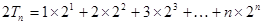 .② 10分
.② 10分①
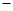 ②得
②得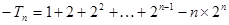 11分
11分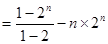 12分
12分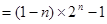 . 13分
. 13分∴
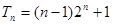 . 14分
. 14分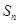 与
与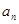 的递推关系的应用,2、错位相减法求数列前
的递推关系的应用,2、错位相减法求数列前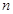 项和.
项和.
练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
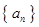 是各项均不为0的等差数列,公差为
是各项均不为0的等差数列,公差为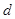 ,
,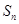 为其前n项和,且满足
为其前n项和,且满足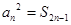 ,
,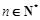 .数列
.数列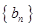 满足
满足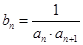 ,
,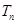 为数列
为数列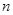 项和.
项和.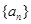 的通项公式
的通项公式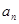 ;
;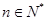 ,不等式
,不等式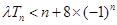 恒成立,求实数
恒成立,求实数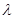 的取值范围;
的取值范围;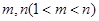 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有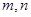
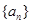 ,
,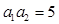 ,
,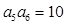 ,则
,则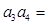 ( )
( ) 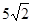
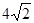
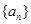 中,
中, 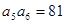 ,则
,则 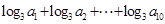 的值是( )
的值是( ) 的首项是
的首项是 ,公比为
,公比为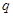 ,
, 是其前
是其前 项和,则
项和,则 的公比为
的公比为 ,则“
,则“ ”是“
”是“ 中,
中, .当
.当 取最小值时,数列
取最小值时,数列 是各项均为正数的等比数列,
是各项均为正数的等比数列, ,则
,则

 的各项均为正数,且
的各项均为正数,且 ,则
,则 为( )
为( )