题目内容
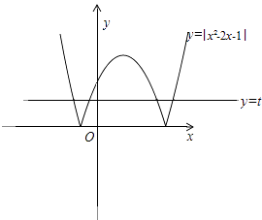
【题目】若方程|x2﹣2x﹣1|﹣t=0有四个不同的实数根x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则2(x4﹣x1)+(x3﹣x2)的取值范围是 .
【答案】(4 ![]() ,8+2
,8+2 ![]() )
)
【解析】解:如图,由|x2﹣2x﹣1|﹣t=0得到:t=|(x﹣1)2﹣2|,则0<t<2. ∴2<2+t<4.0<2﹣t<2.
∴4 ![]() <4
<4 ![]() <8,0<2
<8,0<2 ![]() <2
<2 ![]() ,
,
∴4 ![]() <4
<4 ![]() +2
+2 ![]() <8+2
<8+2 ![]() .
.
∵方程|x2﹣2x﹣1|﹣t=0有四个不同的实数根x1 , x2 , x3 , x4 , x1<x2<x3<x4 ,
∴x1+x4=x2+x3=2,x1x4=﹣1﹣t,x2x3=﹣1+t,
∴2(x4﹣x1)+(x3﹣x2)
=2 ![]() +
+ ![]()
=2 ![]() +
+ ![]()
=4 ![]() +2
+2 ![]() ,
,
∴4 ![]() <2(x4﹣x1)+(x3﹣x2)<8+2
<2(x4﹣x1)+(x3﹣x2)<8+2 ![]() .
.
故答案是:(4 ![]() ,8+2
,8+2 ![]() ).
).
【考点精析】解答此题的关键在于理解函数的零点与方程根的关系的相关知识,掌握二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目