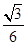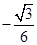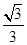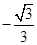题目内容
在正四棱柱ABCDA1B1C1D1中,AA1=2AB,E为AA1的中点,则异面直线BE与CD1所成角的余弦值为( )
A. | B. | C. | D. |
C
解析

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
正四面体ABCD的棱长为1,其中线段AB 平面
平面 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面 上的射影
上的射影 长的范围是( )
长的范围是( )
A.[0, ] ] | B.[ , , ] ] |
C.[ , , ] ] | D.[ , , ] ] |
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是( )
| A.PB⊥AD |
| B.平面PAB⊥平面PBC |
| C.直线BC∥平面PAE |
| D.直线PD与平面ABC所成的角为45° |
[2013·广东高考]设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是( )
| A.若α⊥β,m?α,n?β,则m⊥n |
| B.若α∥β,m?α,n?β,则m∥n |
| C.若m⊥n,m?α,n?β,则α⊥β |
| D.若m⊥α,m∥n,n∥β,则α⊥β |
已知m,n是两条不同直线, 是两个不同平面,以下命题正确的是( )
是两个不同平面,以下命题正确的是( )
A.若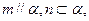 则 则 |
B.若 则 则 |
C.若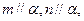 则 则 |
D.若 则 则 |
(2013•浙江)设m、n是两条不同的直线,α、β是两个不同的平面,( )
| A.若m∥α,n∥α,则m∥n | B.若m∥α,m∥β,则α∥β | C.若m∥n,m⊥α,则n⊥α | D.若m∥α,α⊥β,则m⊥β |
设 是不同的直线,
是不同的直线, 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
①若 ,
, ,则
,则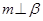
②若 ,
, ,则
,则
③若 ,
,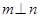 ,则
,则
④若 ,
, ,则
,则 .
.
其中真命题的序号为( )
| A.①③ | B.②③ | C.①④ | D.②④ |