题目内容
已知圆 的圆心在直线
的圆心在直线 上,且与
上,且与 轴交于两点
轴交于两点 ,
, .
.
(1)求圆 的方程;
的方程;
(2)求过点
 的圆
的圆 的切线方程.
的切线方程.
(1)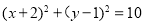 ;(2)
;(2)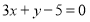 .
.
【解析】
试题分析:(1)先联立直线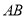 的中垂线方程与直线方程
的中垂线方程与直线方程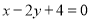 ,求出交点的坐标即圆心
,求出交点的坐标即圆心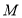 的坐标,然后再计算出
的坐标,然后再计算出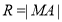 ,最后就可写出圆
,最后就可写出圆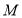 的标准方程;(2)求过点的圆的切线方程问题,先判断点
的标准方程;(2)求过点的圆的切线方程问题,先判断点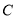 在圆
在圆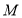 上还是在圆
上还是在圆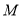 外,若点
外,若点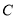 在圆
在圆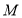 上,则所求直线的斜率为
上,则所求直线的斜率为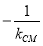 ,由点斜式即可写出切线的方程,若点
,由点斜式即可写出切线的方程,若点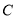 在圆
在圆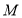 外,则可设切线方程为
外,则可设切线方程为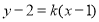 (此时注意验证斜率不存在的情形),然后由圆心
(此时注意验证斜率不存在的情形),然后由圆心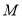 到切线的距离等于半径,求出
到切线的距离等于半径,求出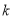 即可求出切线的方程.
即可求出切线的方程.
试题解析:(1)因为圆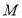 与
与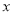 轴交于两点
轴交于两点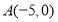 ,
,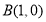 ,所以圆心在直线
,所以圆心在直线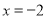 上
上
由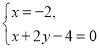 得
得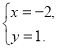 即圆心
即圆心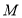 的坐标为
的坐标为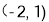 2分
2分
半径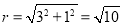
所以圆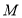 的方程为
的方程为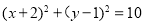 4分
4分
(2)由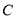 坐标可知点
坐标可知点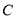 在圆
在圆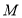 上,由
上,由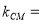
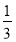 ,可知切线的斜率为
,可知切线的斜率为 6分
6分
故过点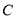
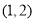 的圆
的圆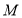 的切线方程为
的切线方程为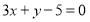 8分.
8分.
考点:1.圆的方程;2.直线与圆的位置关系.

练习册系列答案
相关题目