题目内容
已知数列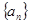 中,
中, 且点
且点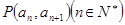 在直线
在直线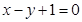 上。
上。
(1)求数列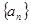 的通项公式;
的通项公式;
 (2)
(2)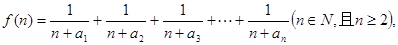 求函数
求函数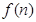 的最小值;
的最小值;
(3)设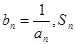 表示数列
表示数列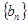 的前
的前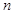 项和。试问:是否存在关于
项和。试问:是否存在关于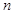 的整式
的整式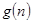 ,使得
,使得
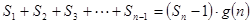 对于一切不小于2的自然数
对于一切不小于2的自然数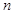 恒成立?若存在,写出
恒成立?若存在,写出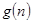 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
【答案】
(1) 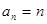
(2) 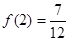
(3) 存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立
【解析】
试题分析:解:(1)由点P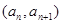 在直线
在直线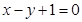 上,
上,
即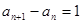 ,
2分
,
2分
且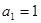 ,数列{
,数列{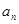 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列
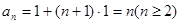 ,
,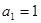 同样满足,所以
同样满足,所以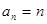 4分
4分
(2)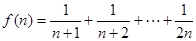
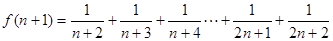 6分
6分
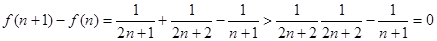
所以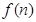 是单调递增,故
是单调递增,故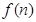 的最小值是
的最小值是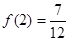 10分
10分
(3)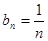 ,可得
,可得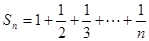 ,
,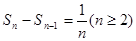 12分
12分
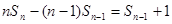 ,
,
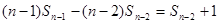
……
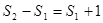
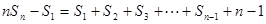
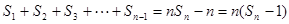 ,n≥2
14分
,n≥2
14分
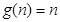
故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立 16分
考点:数列的通项公式,数列的求和
点评:解决的关键是根据已知的递推关系来构造特殊数列来求解,同时能利用定义法判定单调性,确定最值,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目