题目内容
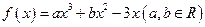
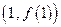
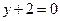
⑴求函数
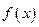 的解析式;
的解析式;⑵若对于区间
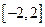 上任意两个自变量的值
上任意两个自变量的值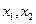 都有
都有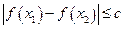 ,求实数
,求实数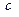 的最小值;
的最小值;⑶若过点
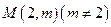 可作曲线
可作曲线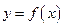 的三条切线,求实数
的三条切线,求实数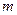 的取值范围
的取值范围(1) (2)
(2) 的最小值为4(3)
的最小值为4(3)
 (2)
(2) 的最小值为4(3)
的最小值为4(3)
⑴ .……………………………………………2分
.……………………………………………2分
根据题意,得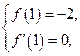 即
即 解得
解得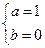 ……………………3分
……………………3分
所以 .………………………………………………4分
.………………………………………………4分
⑵令 ,即
,即 .得
.得 .
.
因为 ,
,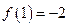 ,
,
所以当 时,
时, ,
,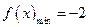 .……………………6分
.……………………6分
则对于区间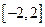 上任意两个自变量的值
上任意两个自变量的值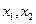 ,都有
,都有
 ,所以
,所以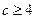 .
.
所以 的最小值为4.……………………………………………………………………8分
的最小值为4.……………………………………………………………………8分
⑶因为点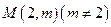 不在曲线
不在曲线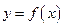 上,所以可设切点为
上,所以可设切点为 .
.
则 .
.
因为 ,所以切线的斜率为
,所以切线的斜率为 .………………………………9分
.………………………………9分
则 =
=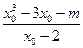 ,………………………………………………………………11分
,………………………………………………………………11分
即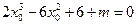 .
.
因为过点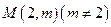 可作曲线
可作曲线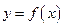 的三条切线,
的三条切线,
所以方程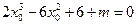 有三个不同的实数解.
有三个不同的实数解.
所以函数 有三个不同的零点.
有三个不同的零点.
则 .令
.令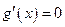 ,则
,则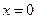 或
或 .
.
则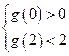 ,即
,即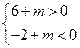 ,解得
,解得 .…………………………………16分
.…………………………………16分
 .……………………………………………2分
.……………………………………………2分根据题意,得
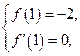 即
即 解得
解得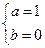 ……………………3分
……………………3分所以
 .………………………………………………4分
.………………………………………………4分⑵令
 ,即
,即 .得
.得 .
. | 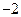 |  |  |  | 1 |  | 2 |
 | | + | | 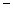 | | + | |
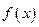 | 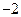 | 增 | 极大值 | 减 | 极小值 | 增 | 2 |
因为
 ,
,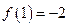 ,
,所以当
 时,
时, ,
,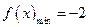 .……………………6分
.……………………6分则对于区间
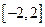 上任意两个自变量的值
上任意两个自变量的值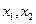 ,都有
,都有 ,所以
,所以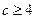 .
.所以
 的最小值为4.……………………………………………………………………8分
的最小值为4.……………………………………………………………………8分⑶因为点
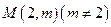 不在曲线
不在曲线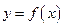 上,所以可设切点为
上,所以可设切点为 .
.则
 .
.因为
 ,所以切线的斜率为
,所以切线的斜率为 .………………………………9分
.………………………………9分则
 =
=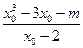 ,………………………………………………………………11分
,………………………………………………………………11分即
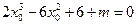 .
.因为过点
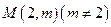 可作曲线
可作曲线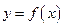 的三条切线,
的三条切线,所以方程
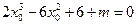 有三个不同的实数解.
有三个不同的实数解.所以函数
 有三个不同的零点.
有三个不同的零点.则
 .令
.令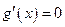 ,则
,则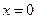 或
或 .
. |  | 0 | 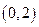 | 2 |  |
 | + | | 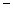 | | + |
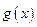 | 增 | 极大值 | 减 | 极小值 | 增 |
则
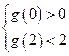 ,即
,即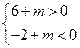 ,解得
,解得 .…………………………………16分
.…………………………………16分
练习册系列答案
相关题目
 沿x轴正向平移1个单位后所得到圆C,则圆C的方程是________,若过点(3,0)的直线
沿x轴正向平移1个单位后所得到圆C,则圆C的方程是________,若过点(3,0)的直线 和圆C相切,则直线
和圆C相切,则直线
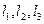


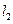
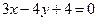 ,求直线
,求直线 的方程。
的方程。 的方程.
的方程.




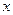

 与
与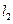 的方程分别为
的方程分别为 ,
, ,直线
,直线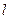 平行于
平行于 ,
, ,且
,且 ,求直线
,求直线