题目内容
已知f (x)＝
sin2x-cos2-
,I(x∈R).
(Ⅰ)求函数f (x)的最小值和最小正周期；
(Ⅱ)设
ABC的内角A、B、C的对边分别为a、b、c，且c＝
，f (C)=0，若向量m＝(1,sinA)与向量n＝(2,sinB)共线，求a，b的值.
（1）f (x)的最小值是-2，最小正周期是T=
=π.（2）a=1，b=2.
解析:
(Ⅰ) f (x)=
sin2x-
-
=sin(2x-
)-1 则f (x)的最小值是-2，
最小正周期是T=
=π.
(Ⅱ) f (C)=sin(2C-)-1=0，则sin(2C-)=1，
∵0＜C＜π，∴0＜2C＜2π，∴-＜2C-＜
π，
∴2C-=
，C =
，
∵向量m=(1,sinA)与向量n=(2,sinB)共线
∴
=
， 由正弦定理得，
= ①
由余弦定理得，c2 =a2 +b2 -2abcos，即3=a2 +b2 –ab ②
由①②解得a=1，b=2.
练习册系列答案
相关题目
xcos2θ
－sin4
)，(a＞0且a≠1)，确定函数的奇偶性、单调性．
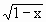，化简f(sin2θ)＋f[sin(－2θ)]，其中0＜θ＜π．
]
，求sin2α的值．
，当θ∈(
π，
π)时，f (sin2θ)－f (－sin2θ)可化简为