题目内容
已知甲、乙两煤矿每年的产量分别为200万吨和300万吨,需经过东车站和西车站两个车站运往外地,东车站每年最多能运280万吨煤,西车站每年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨.要使总运费最少,煤矿应怎样编制调运方案?分析:我们可以将调动方案中,甲煤矿向东站运的煤设为x万吨,乙煤矿向东站运的煤设为y万吨,则我们不难得到关于x,y的不等式组,即约束条件,和目标函数的解析式,再根据约束条件我们画出可行域,然后根据线性规划的解题方法,我们不得得到结果.
解答: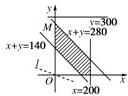 解:设甲煤矿向东车站运x万吨煤,乙煤矿向东车站运y万吨煤,
解:设甲煤矿向东车站运x万吨煤,乙煤矿向东车站运y万吨煤,
那么总运费z=x+1.5(200-x)+0.8y+1.6(300-y)(万元),
即z=780-0.5x-0.8y.
x、y应满足
作出上面的不等式组所表示的平面区域如图所示.
设直线x+y=280与y轴的交点为M,则M(0,280),
把直线l:0.5x+0.8y=0向上平移至经过点M时,z的值最小.
∵点M的坐标为(0,280),
∴甲煤矿生产的煤全部运往西车站,乙煤矿向东车站运280万吨、向西车站运20万吨时,总运费最少.
 解:设甲煤矿向东车站运x万吨煤,乙煤矿向东车站运y万吨煤,
解:设甲煤矿向东车站运x万吨煤,乙煤矿向东车站运y万吨煤,那么总运费z=x+1.5(200-x)+0.8y+1.6(300-y)(万元),
即z=780-0.5x-0.8y.
x、y应满足
|
作出上面的不等式组所表示的平面区域如图所示.
设直线x+y=280与y轴的交点为M,则M(0,280),
把直线l:0.5x+0.8y=0向上平移至经过点M时,z的值最小.
∵点M的坐标为(0,280),
∴甲煤矿生产的煤全部运往西车站,乙煤矿向东车站运280万吨、向西车站运20万吨时,总运费最少.
点评:用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键,可先将题目中的量分类、列出表格,理清头绪,然后列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数.然后将可行域各角点的值一一代入,最后比较,即可得到目标函数的最优解.、

练习册系列答案
相关题目