题目内容
在△ABC中,A=45°,AC=4,AB= ,那么cosB=( )
,那么cosB=( )
A. | B. | C. | D. |
D
解析试题分析:根据题意,由于A=45°,AC=4,AB= ,则根据余弦定理可知
,则根据余弦定理可知 ,然后结合余弦定理可知cosB=
,然后结合余弦定理可知cosB=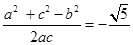 ,故选D.
,故选D.
考点:余弦定理的运用
点评:解决的关键是根据已知的边和角结合正弦定理和余弦定理来求解,属于基础题。

练习册系列答案
相关题目
若△ 的三个内角满足
的三个内角满足 ,则△
,则△
| A.一定是锐角三角形 |
| B.一定是直角三角形 |
| C.一定是钝角三角形 |
| D.可能是锐角三角形,也可能是钝角三角形 |
在 中,已知
中,已知 ,则这个三角形解的情况是( )
,则这个三角形解的情况是( )
| A.有一个解 | B.有两个解 | C.无解 | D.不能确定 |
在△ABC中,若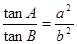 ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.直角三角形 | B.等腰或直角三角形 |
| C.不能确定 | D.等腰三角形 |
边长为 的三角形的最大角与最小角的和是( )
的三角形的最大角与最小角的和是( )
A.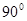 | B.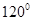 | C.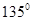 | D.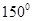 |
在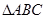 中,
中, ,则
,则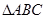 为( )
为( )
| A.直角 三角形 | B.等腰三角形 |
| C.等腰直角三角形 | D.等腰或直角三角形 |
若△ABC能被一条直线分成两个与自身相似的三角形,那么这个三角形的形状是( )
| A.钝角三角形 | B.直角三角形 |
| C.锐角三角形 | D.不能确定 |
已知 ,则
,则 =( )
=( )
| A.4 | B.5 | C.6 | D.7 |
如图,在地面 处测得树梢的仰角为60°,
处测得树梢的仰角为60°, 与树底部
与树底部 相距为5米,则树高为( )
相距为5米,则树高为( )
A. 米 米 | B.5米 | C.10米 | D. 米 米 |