题目内容
在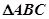 中,根据下列条件解三角形,其中有两个解的是( )
中,根据下列条件解三角形,其中有两个解的是( )
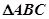 中,根据下列条件解三角形,其中有两个解的是( )
中,根据下列条件解三角形,其中有两个解的是( )| A.b="10," A=450, C=600 | B.a=6, c=5, B=600 |
| C.a=7, b=5, A=600 | D.a=14, b="16," A=450 |
C
A、由A和C的度数,利用三角形的内角和定理求出B的度数,从而得到sinA,sinB及sinC的值,再由b的值,利用正弦定理求出a与c的值,本选项只有一解;
B、由a,c及cosB的值,利用余弦定理求出b的值,再利用余弦定理表示出cosC,发现其值小于0,即C为钝角,c为最大边,故本选项只有一解;
D、由a,b及sinA的值,利用正弦定理求出sinB的值,由A为钝角,即为三角形的最大角,得到B只有一解,从而求出c也只有一解;
C、由a,b及sinA,利用正弦定理求出sinB的值,再由B的范围,利用特殊角的三角函数值即可求出B有两解,本选项有两解.
B、由a,c及cosB的值,利用余弦定理求出b的值,再利用余弦定理表示出cosC,发现其值小于0,即C为钝角,c为最大边,故本选项只有一解;
D、由a,b及sinA的值,利用正弦定理求出sinB的值,由A为钝角,即为三角形的最大角,得到B只有一解,从而求出c也只有一解;
C、由a,b及sinA,利用正弦定理求出sinB的值,再由B的范围,利用特殊角的三角函数值即可求出B有两解,本选项有两解.

练习册系列答案
相关题目
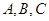 所对的边分别是
所对的边分别是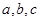 .若
.若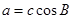 ,则△ABC是
,则△ABC是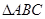 中,∠A、∠B的对边分别为a,b,且∠A=60°,
中,∠A、∠B的对边分别为a,b,且∠A=60°,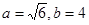 ,那么满足条件的
,那么满足条件的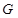 为△
为△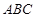 的重心,且
的重心,且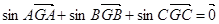 ,则
,则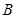 的大小为
的大小为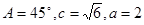 的△ABC的个数为m,则am的值为
的△ABC的个数为m,则am的值为 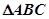 三个内角
三个内角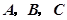 的对边分别为
的对边分别为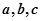 ,若
,若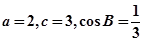 ,
, 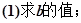
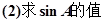
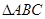 的三个内角满足
的三个内角满足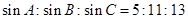 ,则
,则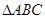 中,
中,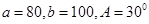 ,则
,则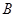 的解的个数是 ( )
的解的个数是 ( ) 中,
中,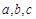 分别为
分别为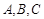 的对边,若
的对边,若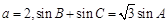 ,且
,且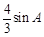 ,则角
,则角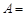 ________
________