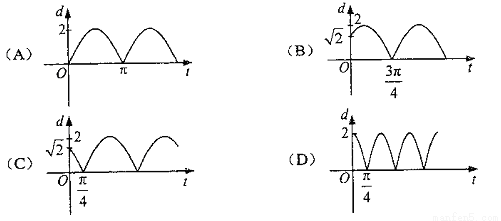题目内容
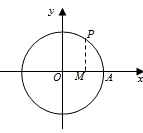如图，质点P在半径为10cm的圆上逆时针作匀速圆周运动，角速度为2rad/s，设A（10，0）为起始点，则时刻t=2时，点P在x轴上的射影点M的速度________cm/s．
-20sin4
分析：由题意求出点P在x轴上的射影点M到原点的距离的表达式，利用导数求出本题的结果．
解答：由题意可知：点P在x轴上的射影点M到原点的距离为y=10cos2t，
所以点P在x轴上的射影点M的速度为：v=y′=-20sin2t，
所以时刻t=2时，点P在x轴上的射影点M的速度为：-20sin4 cm/s．
故答案为：-20sin4．
点评：本题是基础题，考查三角函数的表达式的求法，函数导数的应用，考查计算能力．
分析：由题意求出点P在x轴上的射影点M到原点的距离的表达式，利用导数求出本题的结果．
解答：由题意可知：点P在x轴上的射影点M到原点的距离为y=10cos2t，
所以点P在x轴上的射影点M的速度为：v=y′=-20sin2t，
所以时刻t=2时，点P在x轴上的射影点M的速度为：-20sin4 cm/s．
故答案为：-20sin4．
点评：本题是基础题，考查三角函数的表达式的求法，函数导数的应用，考查计算能力．
练习册系列答案
相关题目
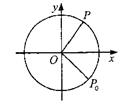
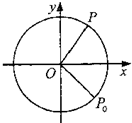如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0（
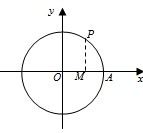12、如图，质点P在半径为10cm的圆上逆时针作匀速圆周运动，角速度为2rad/s，设A（10，0）为起始点，则时刻t=2时，点P在x轴上的射影点M的速度
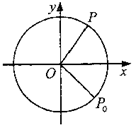如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0（
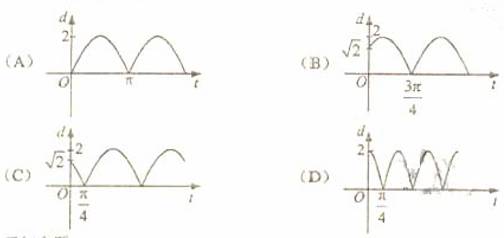如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0（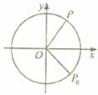
，-
（
，-
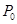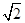