题目内容
(本小题共10分)
已知函数
(1)解关于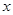 的不等式
的不等式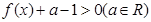 ;
;
(2)若函数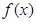 的图象恒在函数
的图象恒在函数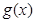 图象的上方(没有公共点),求
图象的上方(没有公共点),求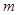 的取值范围。
的取值范围。
【答案】
(1)当a=1时,解集为(-∞,2)∪(2,+∞);当a>1时,解集为R,当a<1时,解集为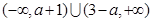 ;(2)
;(2)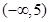
【解析】
试题分析:(Ⅰ)不等式f(x)+a-1>0即为|x-2|+a-1>0,
当a=1时,解集为x≠2,即(-∞,2)∪(2,+∞);
当a>1时,解集为全体实数R;
当a<1时,解集为(-∞,a+1)∪(3-a,+∞).
(Ⅱ)f(x)的图象恒在函数g(x)图象的上方,即为|x-2|>-|x+3|+m对任意实数x恒成立,即|x-2|+|x+3|>m恒成立,(7分)
又由不等式的性质,对任意实数x恒有|x-2|+|x+3|≥|(x-2)-(x+3)|=5,于是得m<5,
故m的取值范围是(-∞,5).
考点:本题考查了绝对值不等式的解法及恒成立问题
点评:在解答含有绝对值不等式问题时,要注意分段讨论来取绝对值符号的及利用绝对值的几何意义来求含有多个绝对值的最值问题

练习册系列答案
相关题目

 的三个角
的三个角 的对边分别为
的对边分别为 ,且
,且 。数列
。数列 是等比数列,且首项
是等比数列,且首项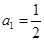 ,公比为
,公比为 。
。 ,求数列
,求数列 的前
的前 项和
项和 。
。 ,且
,且 ,求
,求
 ,
, B=
B= ,C=
,C=
 C,求m的取值范围。
C,求m的取值范围。 为等差数列,且
为等差数列,且 ,
, 。
。 满足
满足 ,
, ,求
,求